真空跃迁与泡泡生成
量子力学的半经典解释
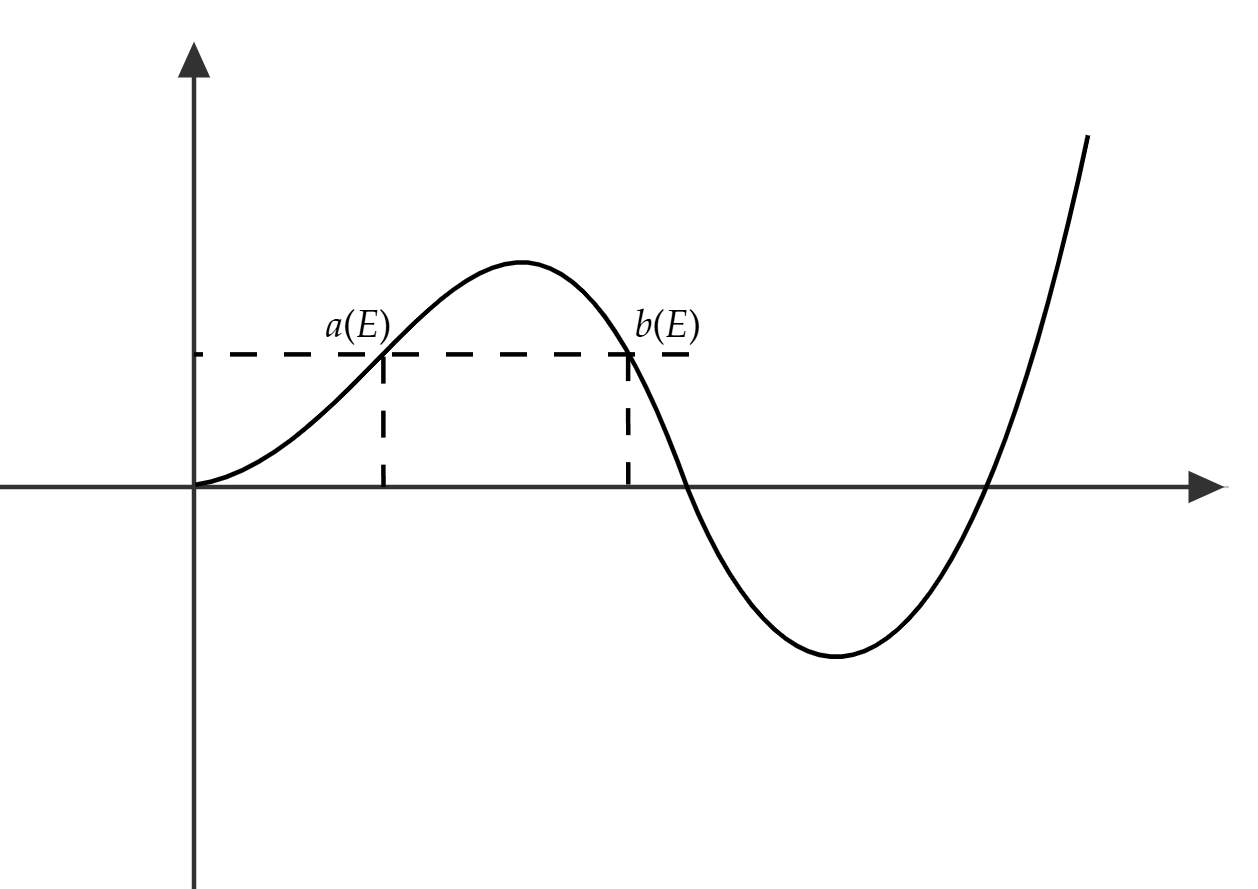
让我们先从一维非相对论的情况开始。在如图势场下,粒子在$t=0$时刻位于$x=0$势阱内(虽然这样的说法很不严谨,意会一下),且能量低于势垒高度。那么粒子只能通过量子隧穿来从势阱中逃逸。在半经典的WKB近似下,该粒子的波函数可以写为$\psi \sim \exp(i \int \sqrt{2m(E-V)}\dd x) = \exp(iS)$,这里的$S$即是作用量。在经典允许区,波函数振荡。而在势垒内部波函数指数衰减。在$x>b$的区域,波函数相比于势阱内的值有一个指数的压低$\abs{\psi}^2 \sim \exp(-\int_a^b \sqrt{2m(V-E) }\dd x)$,也就有隧穿的概率是被该项指数压低的
零温与有限温度下的真空跃迁率
现在让我们来考虑在零温下的一个具有多个局域极小值的势的标量场$\phi$,作用量为
$$ S=\int \dd[4]x ~ \left(\frac{1}{2} (\partial_\mu \phi)(\partial^\mu \phi) - V \right) $$
现在我们考虑从假真空$\phi_F$到真真空$\phi_T$的跃迁概率的计算。由于势能的绝对值具有任意性,在下面的讨论中我们扣除掉无限大的真空能,而将假真空$\phi_F$处的势能$V(\phi_F)$设定为0(也就是重定义$V(\phi) \to V(\phi)-V(\phi_F)$)。
由于我们不知道假真空会跃迁到哪个位置,比如在过冷相变中,真真空所在的势阱可能非常深,假真空跃迁的情景更可能是跃迁到真真空势阱的坡上,再在新真空的势阱中振荡到最低点。在这种问题上,正规的流程是使用初态-初态振幅法。
$$ \left\langle\phi_f, t_f \mid \phi_i, t_i\right\rangle=\int \mathcal{D} \phi~ e^{i S[\phi]} $$
由于指数中是 $i S[\phi]$ ,而$S$为一实数,于是指数项是振荡的,这对我们积分造成了很大困难。于是我们需要进行Wick转动 $t \to i \tau$,于是有
$$ S = i \int \dd[3]x \dd \tau ~\left(\frac{1}{2} (\frac{\partial \phi}{\partial \tau})^2 + \frac{1}{2} \nabla^2 \phi + V \right) = i S_E $$
这里的$S_E$也即是欧几里得空间的作用量,度规为++++。可以注意到,在欧几里得空间的势能前面的符号是加号,也就相当于具有一个“倒转的势能”。这一做法相当于将量子跃迁变为了经典的下滚的过程。
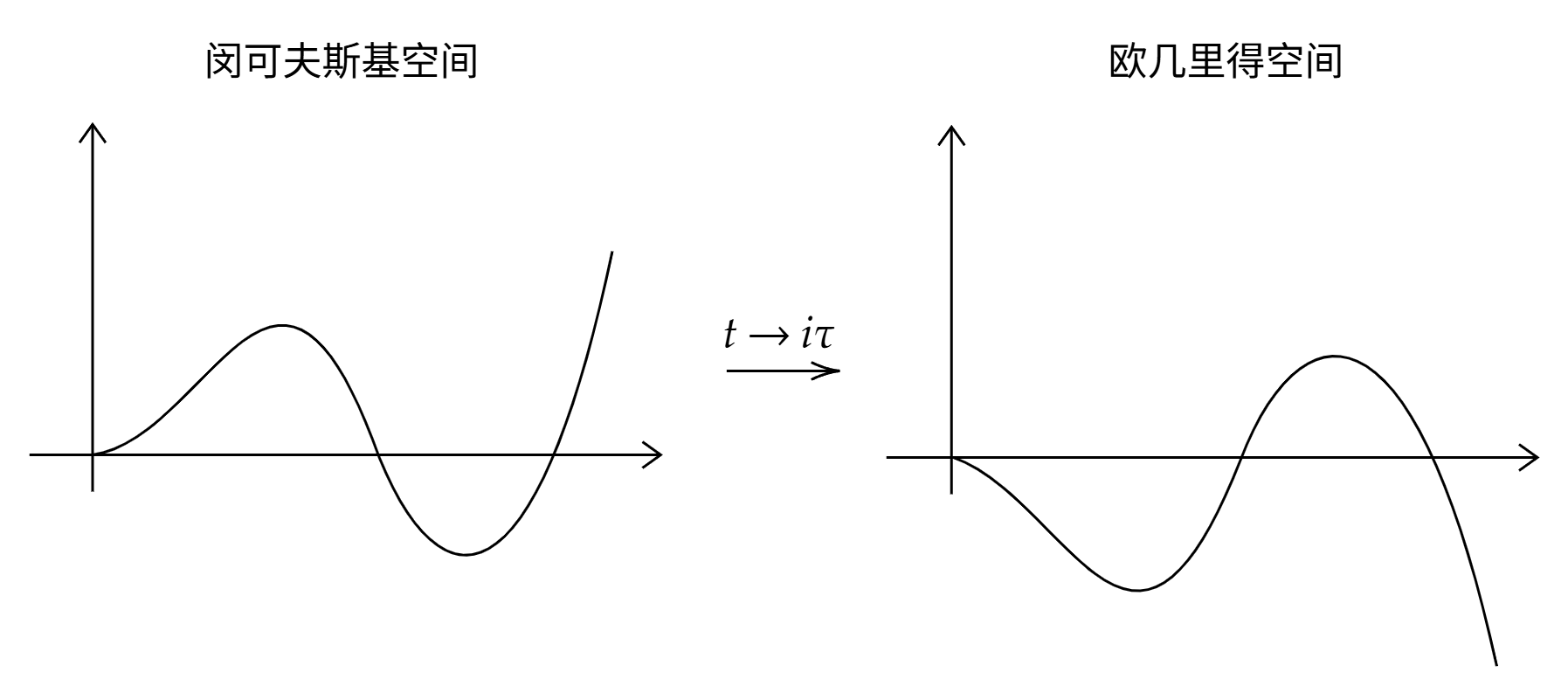
观察作用量的形式,不难发现原先在闵可夫斯基空间下具有SO(1,3)对称性变为了欧几里得空间下的O(4)对称性。于是我们可以做变量代换$r=\sqrt{x^2+t^2}$,同时为了突出对称性以及和下文对比,将这里的具有O(4)对称性的作用量记为$S_4$:
$$ S_4= 2\pi^2 \int_0^\infty \dd r~ r^3 ~\left(\frac{1}{2} (\frac{\partial \phi}{\partial r})^2 + V \right) $$
由于现在粒子有一经典的路径发生跃迁,那么跃迁振幅的主要贡献即为该经典路径的贡献。于是从假真空到真真空的跃迁概率为
$$ \Gamma \propto \exp(-S_4) $$
而这里的$S_4$的积分就是通过经典的运动方程的解的路径进行。运动方程不难得到
$$ \frac{\dd[2] \phi}{\dd r^2}+\frac{3}{r} \frac{\dd \phi}{\dd r}=V^{\prime}(\phi, 0) $$
这个解被称为 bounce 解,具体的将在下一节介绍。(bounce 这个名字来源于 Coleman1977,由于在严谨的分析中,跃迁概率的积分路径相当于从$\phi=0$积分到某个值,然后再倒转回去,就像一个小球在倒转势中被抛了出去,撞上了势阱又被反弹回来,所以被称为 bounce)
在上面我们只考虑了经典路径的贡献,得出了$\Gamma \propto \exp(-S_4)$。但是其实量子涨落是不可忽略的。我们需要对经典路径附近的量子涨落进行计算。在这里我们略去计算过程,直接给出结果
$$ \Gamma = \left( \frac{S_4}{2\pi} \right)^2 \abs{\frac{det'[-\partial^2 +V''(\phi)]}{det'[-\partial^2 +V''(0)]}}^{-1/2} \exp(-S_4) $$
同时我们需要注意到,跃迁概率应当是量纲为4的量,在上面的表达式中,其实量纲隐含在了泛函行列式里。而该泛函行列式的计算十分困难,我们可以通过量纲分析的方法,将该行列式替换掉。瞬子解在四维时空中是球对称的,而解具有一个特征尺度,也就是真空泡泡的半径$R_0$,于是这个泡泡在四维时空的体积$\sim R_0^{-4}$。衰变率作为单位时空体积内的概率,其尺度必然与该体积相关,于是我们可以预期跃迁概率的指数前系数$A \propto R_0^{-4}$。那么基于以上讨论,我们可以写出便于计算的跃迁概率的表达式
$$ \Gamma = R_0^{-4} \left( \frac{S_4}{2\pi} \right)^2 \exp(-S_4) $$
现在让我们来看有限温度下的情况。在有限温度下,由于周期性边界条件$\beta=1/T$的存在,当$T>>R_0$时,时间维度的$\beta$小于 bounce 解的半径,那么则可以直接将时间部分积出来。
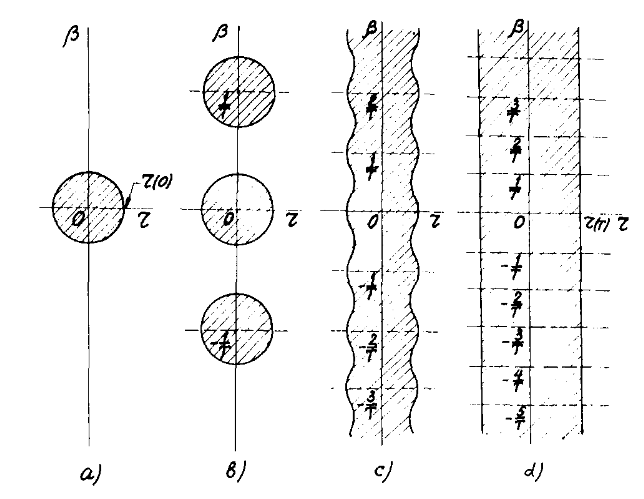
于是这种情况下,我们可以直接写出跃迁概率和作用量
$$ S_3 = \int \dd[3]x ~\left( \frac{1}{2} \nabla^2 \phi + V(\phi,T) \right) $$
$$ \Gamma \sim \exp(-S_3/T) $$
现在作用量具有O(3)对称性,这也是角标的3的原因。在球坐标下,有
$$ S_3= 4\pi \int_0^\infty \dd r~ r^2 ~\left(\frac{1}{2} (\frac{\partial \phi}{\partial r})^2 + V \right) $$
运动方程则为
$$ \frac{\dd[2] \phi}{\dd r^2}+\frac{2}{r} \frac{\dd \phi}{\dd r}=V^{\prime}(\phi, T) $$
和零温下的只相差一个系数。
同样的,如果严谨地计算经典路径附近的量子涨落的话,我们能够得到跃迁概率的严格表达式
$$ \Gamma(T)=T\left(\frac{S_3}{2 \pi T}\right)^{3 / 2} \abs{\frac{det'[-\partial^2 +V''(\phi)]}{det'[-\partial^2 +V''(0)]}}^{-1/2} \exp({-S_3 / T}) $$
同样的,跃迁概率是量纲为4的量,空间上的量纲3隐含在了泛函行列式里。由于在高温极限$T>> R_0^{-1}$下,粒子质量$m$、bounce解半径$R_0$、势垒能标都远远小于温度,所以此时温度$T$成为了体系唯一的能量尺度。于是我们可以预期跃迁概率的指数前系数$A \propto T^4$。那么基于以上讨论,我们可以写出便于计算的跃迁概率的表达式
$$ \Gamma(T)=T^4 \left(\frac{S_3}{2 \pi T}\right)^{3 / 2} \exp({-S_3 / T}) $$
bounce 解的运动方程解与薄膜近似
现在让我们来求解运动方程。在有限温度和零温下的运动方程形式是一致的
$$ \frac{\dd[2] \phi}{\dd r^2}+\frac{D-1}{r} \frac{\dd \phi}{\dd r}=V^{\prime}(\phi, T) $$
在$T=0$时,$D=4$;在$T>>0$时,$D=3$。
我们先来考虑这个解大致是长怎样的。当时空中的某一点发生跃迁后,该点和附近的区域的场值$\phi$都在新真空$\phi_T$处,而远处还停留在假真空$\phi_F$处。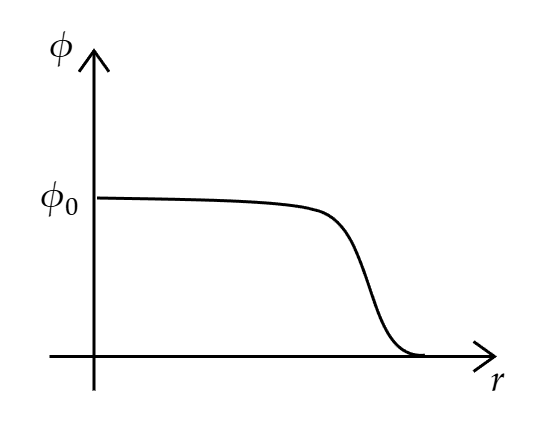
于是这对我们求解运动方程施加了两个边界条件
$$ \begin{aligned} \frac{\dd \phi}{\dd r}|_{r=0}=0\\ \phi|_{r=\infty}=\phi_F \end{aligned} $$
我们求解运动方程的目的是为了计算跃迁概率,也就是计算作用量的积分。由于在$\phi=\phi_F$的区域,无论是导数还是势能都为0(如果我们已经对势能进行了平移了,也即扣除掉无穷大的真空能了),于是作用量的积分相当于有一上限$R_0$。
当真空泡泡的半径很大时,泡泡的“下降沿”和半径相比很小时,我们可以将三/四维问题近似为一个一维问题,也即运动方程可以近似为
$$ \frac{\dd[2] \phi}{\dd r^2}=V^{\prime}(\phi, T) $$
这正是一个一维平坦畴壁的运动方程。这被称为是薄壁近似。
这个运动方程可以巧妙地化为一阶方程,将运动方程两边同时乘以 $\frac{d \phi}{d r}$ :
$$ \frac{\dd \phi}{d r} \frac{\dd[2] \phi}{\dd z^2}=\frac{\dd V(\phi)}{\dd \phi} \frac{\dd \phi}{\dd r} $$
利用链式法则,上式可以写成:
$$ \frac{d}{d r}\left[\frac{1}{2}\left(\frac{d \phi}{d r}\right)^2\right]=\frac{d}{d r}[V(\phi)] $$
对两侧关于 $r$ 积分,我们得到:
$$ \frac{1}{2}\left(\frac{d \phi}{d r}\right)^2=V(\phi)+C $$
结合边界条件可以得到积分常数$C=0$
于是我们有
$$ \frac{d \phi}{d r}=\sqrt{2 V(\phi)} $$
现在让我们来看作用量的积分。在薄壁近似下,由于泡壁的区域很小,于是我们可以将泡的作用量也即经典能量分为两部分:泡内外能量差和表面张力。
$$ \begin{aligned} S_4(R_0) & =2 \pi^2 \int_0^{R_0} r^3 \dd r\left[\frac{1}{2}\left(\frac{\dd \phi}{\dd r}\right)^2+V(\phi)\right] \\ & =-\frac{1}{2} \varepsilon \pi^2 R_0^4+2 \pi^2 R_0^3 S_1 \end{aligned} $$
$$ \begin{aligned} S_3(R_0) & =4 \pi \int_0^{R_0} r^2 \dd r\left[\frac{1}{2}\left(\frac{\dd \phi}{\dd r}\right)^2+V(\phi, T)\right] \\ & =-\frac{4}{3} \pi R_0^3 \varepsilon+4 \pi R_0^2 S_1(T) \end{aligned} $$
其中$\varepsilon$为能量差密度$\varepsilon=V(\phi_T)-V(\phi_F)$。
而$S_1$即为一维畴壁的作用量
$$ S_1=\int_0^{\infty} \dd r\left[\frac{1}{2}\left(\frac{\dd \phi}{\dd r}\right)^2+V(\phi)\right]=\int_{\phi_F}^{\phi_T} \dd \phi \sqrt{2 V(\phi)} $$
现在,问题则是我们还不知道$R_0$具体是多少。作用量原理要求对于真实的路径,作用量应取极值。于是我们可以得到
$$ R_0 = \frac{(D-1)S_1}{\varepsilon} $$
从这里我们可以看出,薄膜近似的泡泡半径$R_0>>0$的要求是$S_1>>\varepsilon$,也即为假真空和真真空近似简并的情况。而在过冷相变时并不是这样,仍需要借助数值求解。
注:关于数值求解的困难和方法
关于 bounce 解的运动方程求解是一个BVP问题,由于初始条件的限制和方程本身不稳定,导致求解一直是个难题。传统的求解 BVP 的方法为 Shooting 法,但是该方法十分依赖于初始猜测值。下图为数值求解时会遇到的情况。当初始猜测稍大于理论值时,解便会发散;而初始猜测稍小时又会发生振荡。
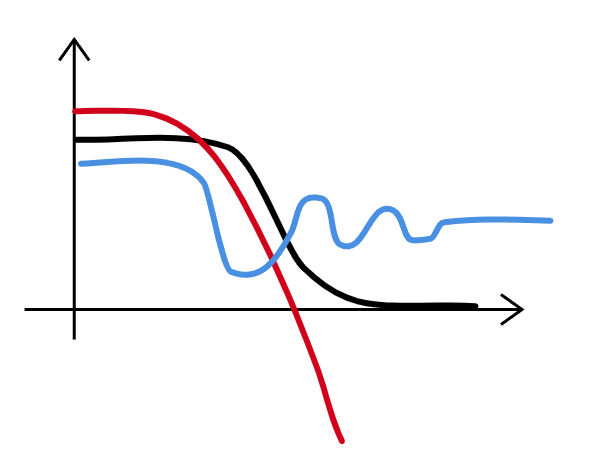
比较好的应对方法为所谓的 over/under shoot,也就是选定一个一定会发生over shoot和一个一定会发生 under shoot的值,然后使用二分法多次进行shooting计算来逼近精确值。
在进行shooting时也需要严格控制ode算法的精度,否则会在二分时miss掉精确值的区间。
相变的热过程
在辐射能为主导的且熵守恒的宇宙中,温度与时间有下式中的关系
$$ \frac{\dd t}{\dd T} = -\frac{1}{T H(T)} $$
对于宇宙学相变的过程,在计算跃迁概率时,取$S_3/T$和$S_4$中较大者的贡献即可。也即
$$ \Gamma(T) \simeq \max \left[T^4 \left(\frac{S_3}{2 \pi T}\right)^{3/2} \exp \left(-S_3 / T\right), ~ R_0^{-4} \left(\frac{S_4}{2 \pi}\right)^2 \exp \left(-S_4\right)\right] $$
在相变的过程中,有一个重要的时间节点成核温度/时间,定义为单位视界平均产生一个泡泡的温度/时间点,也即
$$ N\left(T_n\right)=\int_{t_c}^{t_n} d t \frac{\Gamma(t)}{H(t)^3}=\int_{T_n}^{T_c} \frac{d T}{T} \frac{\Gamma(T)}{H(T)^4}=1 $$
其中$T_c / t_c$为转变温度/时间。以上式子使用了熵守恒进行时间-温度的换算。由于这是一个包含积分的方程,为了简化计算,该定义还可以近似为
$$ \frac{\Gamma(T_n)}{H^4(T_n)} = 1 $$
为了更详细获得宇宙从假真空转变为真真空的演化细节,我们考虑宇宙中随机一点的在某一时刻停留在假真空的概率。单位共动体积中真真空泡泡的体积为
$$ \begin{aligned} I(t) & = \int_{t_c}^t \Gamma(t') a^3(t') \dd t' * \frac{4}{3} \pi r^3(t-t')\\ & =\frac{4 \pi}{3} \int_{t_c}^t \dd t' \Gamma\left(t'\right) a\left(t^{\prime}\right)^3 r\left(t- t^{\prime}\right)^3 \end{aligned} $$
其中$r(t-t')$为$t'$时刻产生的真空泡泡在$t$时刻的半径
$$ r(t-t') = \int_{t'}^t \frac{v_w}{a(\tilde{t})} \dd {\tilde{t}} $$
这里的$v_w$为真空泡泡膨胀速度。由内外能量差和泡壁与外界摩檫力决定,具体的值需要对泡泡内外等离子体的演化进行详细的数值计算。在简单的定性分析中,如果相变足够强,释放的能量足够多,摩檫力始终无法与能量差产生的驱动力相抵,那么泡泡膨胀的速度$v_w$则会迅速接近光速,也即$v_w \sim c $,这也被称为是失控膨胀(Runaway Expansion)。一般而言,过冷的强一级相变即是这种情况。
同样我们可以将以时间为变量改写为以温度为变量的形式
$$ I(T)=\frac{4 \pi v_{w}^{3}}{3} \int_{T}^{T_{c}} \frac{\Gamma\left(T^{\prime}\right) d T^{\prime}}{T^{\prime 4} H\left(T^{\prime}\right)}\left(\int_{T}^{T^{\prime}} \frac{d \tilde{T}}{H(\tilde{T})}\right)^{3} $$
但是积分$I(t)$没有考虑进泡泡间的重合。但是如果我们注意到假真空的体积分数有
$$ P(t+dt)=P(t)+(t\~{}t+\dd t时间假真空减小的体积) $$
而我们假设真空泡泡是在宇宙中均匀出现的话(这其实是宇宙学原理所要求的),那么$t\~{}t+\dd t$时间假真空减小的体积就正比于当前假真空的体积分数$P(t)$乘上单位体积真真空泡泡增加的体积分数$\dd I(t)/\dd t$(相当于我们是在假真空中看真真空增加体积的几率,于是真真空相互重合的区域便被自然的排除了)
也就是有
$$ \frac{\dd P(t)}{\dd t} = -P(t)\frac{\dd I(t)}{\dd t} $$
于是宇宙中随机一点的在某一时刻停留在假真空的概率为
$$ P(t) = e^{-I(t)} $$
当宇宙中开始出现极少量的体积也很小的真空泡泡时,这些泡泡释放出来的能量肯定对于整个宇宙而言微乎其微,并且表现出来的性质只是一种局域的影响。而如果假设宇宙是均匀的话,那么根据渗流理论,在渗流阈值时,新相出现贯穿整个系统的连通,这些新相的影响也不再局域,而是开始影响整个系统,标志为相变发生的时间点。对于三维空间的连续介质,渗流阈值为新相的占据概率为$\phi_c \approx 0.289$。那么对应的也就是发生渗流的渗流温度$T_p$/渗流时间$t_p$有
$$ P(t_p) \sim 0.71,~ I(t_p) \sim 0.34 $$
我们用$T_*$和$t_*$来标记相变开始的时间点。主流的文献大多认为$T_*=T_p$。一般而言,$t_p>t_n$。但是当真空跃迁率十分低的情况下,有可能出现甚至$t_n$不存在的情况,也就是整个宇宙由少数几个泡泡填满。
对于相变结束的时间点,一个十分自然的想法便是宇宙中的假真空占比近乎为0时,也即是当$P(t)<10^{-M}$,$M$是个很大的正数。然而我们需要注意到的是,宇宙是在膨胀中的,所以就有可能出现虽然宇宙中假真空的占比逐渐减小,但是假真空的绝对体积却在增大,只不过比宇宙的膨胀速度慢的可能性。所以为了使宇宙中假真空区域最终收敛到0,需要增加这样一个条件
$$ \frac{1}{a^3 P}\frac{\dd (a^3 P)}{\dd t} = 3H(t) - \frac{\dd I(t)}{\dd t} = H(T) \left (3+T \frac{\dd I(T)}{\dd T} \right) <0 $$
为了计算相变之后宇宙的温度,我们需要先计算相变释放出的潜热。根据热力学原理,能够得到
$$ \Delta \rho = \Delta V - T (\frac{\partial V}{\partial T})_V $$
如果我们将相变潜热对泡泡外的辐射能$\rho_R$进行归一化的话,便有
$$ \alpha(T) = \frac{\Delta V(T) - T (\frac{\partial V}{\partial T})}{\rho_R} $$
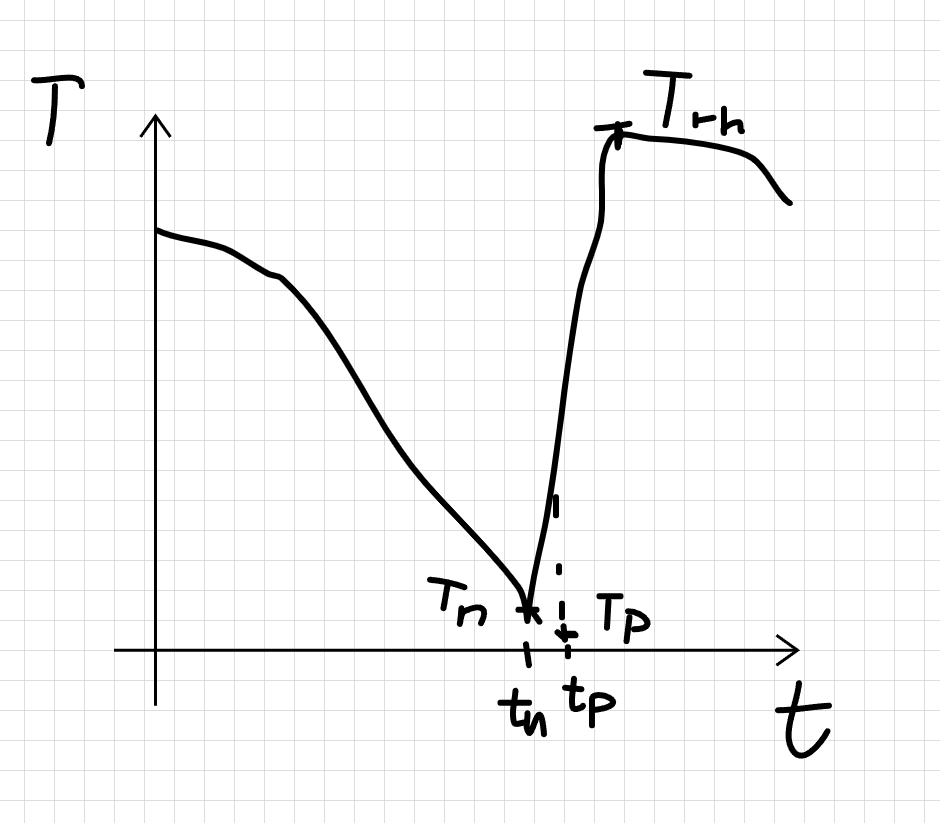
相变后,真空能被释放出来到宇宙,转换为辐射能量,加热整个宇宙。根据能量守恒,如果我们认为相变前后宇宙的自由度变化不大的话,可以得到相变后被加热的宇宙的温度
$$ T_{rh} = [1+\alpha(T_p)]^{1/4} T_p $$
相变引力波
在一级相变的过程中,目前普遍认为有三种引力波的主要来源:
1)泡泡间的相互碰撞:在泡泡膨胀并发生相互碰撞时,碰撞的泡壁中的能量释放出来并产生引力波。这个机制只有在相变潜热主要释放到气泡壁的动能中的情况下才占主导;
2)声波:在大多数情况下,膨胀的气泡壁并不会在真空中传播,而是会推动泡泡外的等离子体,激发出声波。在气泡碰撞并合并后,这些声波并不会立即消失,而会在等离子体中持续传播振荡和相互干涉。这种流体的大尺度、相干的能量密度扰动是极其有效的引力波来源;
3)湍流:声波在传播过程中会逐渐衰减,其能量的一部分会耗散,并转变为等离子体中的湍流,也会作为引力波的来源。湍流产生的引力波通常持续时间比声波更长,并且其能谱的峰值频率与声波不同(通常在更低频)。
$$ \Omega h^2 = \Omega_{col} h^2 + \Omega_{sw} h^2 +\Omega_{turb} h^2 $$
和相变引力波相关的参数
一般而言,用来确定引力波谱的相变的关键参数有泡泡碰撞速度$v_w$,衡量相变强度的参数$\alpha$和衡量相变过程持续时间的参数$\beta/H$(或者可以考虑GW产生的相关长度尺度$\bar R$而不是$\beta$,我们下面会讨论这点),相变释放的能量在等离子体、真空场等方面的比例$\kappa$。下面我们详细讨论这些参数。
相变强度$\alpha$
表征相变强度的$\alpha$,在部分工作中即定义为前面定义的对辐射能进行归一化的相变潜热$\alpha$。但是有工作(1004.4187)指出为了去除辐射修正的影响(也就是只考虑辐射的能动量张量的迹反常,也即$\epsilon-3p$部分),在导数项前面会出现一个$1/4$因子,现在通常使用这一做法,也即
$$ \alpha'(T) = \frac{\Delta V(T) - \frac T 4 (\frac{\partial V}{\partial T})}{\rho_R} $$
相变特征时间$\beta/H_*$和特征尺度$\bar R_* H_*$
在考虑相变持续时间的通常做法(Michael S. Turner, Erick J. Weinberg, and Lawrence M. Widrow, 1992)和(1611.05853),是在相变开始的时间点附近对作用量(在有限温度下即为$S_3/T$)进行多项式展开
$$ S(t) \approx S\left(t_*\right)-\beta\left(t-t_*\right)+\frac{\zeta^2}{2}\left(t-t_*\right)^2+\cdots $$
于是有
$$ \Gamma(t) \approx \Gamma_* e^{\beta\left(t-t_*\right)-\frac{\zeta^2}{2}\left(t-t_*\right)^2+\cdots} $$
$$ \beta=-\left.\frac{\mathrm{d} S}{\mathrm{~d} t}\right|_*, \quad \zeta^2=\left.\frac{\mathrm{d}^2 S}{\mathrm{~d} t^2}\right|_* \quad \text{其中} S=S_4 ~ \text{or} \frac{S_3}{T} $$
$$ \frac{\beta}{H_*}=\left.T_* \frac{\mathrm{~d} S}{\mathrm{~d} T}\right|_* \quad \text{其中} S=S_4 ~ \text{or} \frac{S_3}{T} $$
其中$H_* = H(T_*)$
如果我们只取一阶近似,也就是对$\Gamma(t) = \Gamma_* e^{\beta\left(t-t_*\right)}$,那么这里的$\beta^{-1}$则代表相变过程的时间尺度,于是$\beta/H_*$则代表着哈勃时间尺度与 FOPT 持续时间的比率,也即代表着相变过程的特征时间。
与相变过程的特征时间$\beta/H_*$相对的还有相变过程的特征尺度,也即在相变发生时间点的泡泡的相对于宇宙的视界尺寸的平均半径$\bar R_* H_*$。
在某一时刻的泡泡平均半径$\bar R$可以被定义为$\bar R(t) = [n_b(t)]^{-1/3}$,其中$n_b$为真空泡泡的数密度,可以根据下式计算
$$ n_b(t)=\int_{t_c}^t \mathrm{~d} t^{\prime} P\left(t^{\prime}\right) \Gamma\left(t^{\prime}\right) \frac{a^3\left(t^{\prime}\right)}{a^3(t)} $$
同样可以利用辐射能主导下的时间-温度关系写出以温度为变量的形式
$$ n_b(T) = T^3 \int_{T}^{T_c} \dd T' \frac{\Gamma(T')}{T'^4 H}P(T') $$
对于相变时间持续很短的情况下,也即有$\beta/H>>1$时,$\beta/H_*$和$\bar R_* H_*$存在一比例关系,可以进行互换。$\beta/H_*$ 描述相变过程在时间上有多快(相对于宇宙膨胀时标)。$\bar R_* H_*$ 描述相变产生的结构在空间上有多大(相对于宇宙视界尺度)。由于泡泡的半径可以估算为$R\sim v_w * 相变持续时间$,于是相变的特征时间$\beta/H$与特征尺度$\bar R_* H_*$有一个近似关系$\left( \frac{\beta}{H_*} \right) \sim v_w \left( \bar R_* H_* \right)^{-1}$,当然更加精细的计算结果(2404.00646附录)指出还有一个O(1)的系数
$$ \left( \frac{\beta}{H_*} \right) \approx (8\pi)^{1/3} v_w \left( \bar R_* H_* \right)^{-1} $$
需要注意的是,在相变时间持续较长的情况下,那么对作用量进行线性展开的近似效果就不好了,也即$\beta/H_*$在此时无法作为相变的特征时间使用。这种情况下更好的做法是使用特征尺度$\bar R_* H_*$,并通过定义式进行计算。
泡壁速度$v_w$和能量分数$\kappa$
$v_w \sim 1$的情况下
对于泡壁速度$v_w$,理论上我们需要对泡泡内外的等离子体进行复杂的非平衡态分析(1004.4187 & 2204.13120 & 2205.02492),综合考虑泡泡两侧的热效应和粒子在泡壁的反弹与透射的行为。但是如果只是局限于泡壁速度接近光速的情况(也即是所谓的“Runaway”,过冷相变即很有可能是这种情况,真空能极大导致泡泡可以加速到十分接近光速),可以把问题简化为只考虑泡泡两侧的势能差构成的驱动力和粒子碰撞造成的摩擦力(0903.4099 & 1703.08215)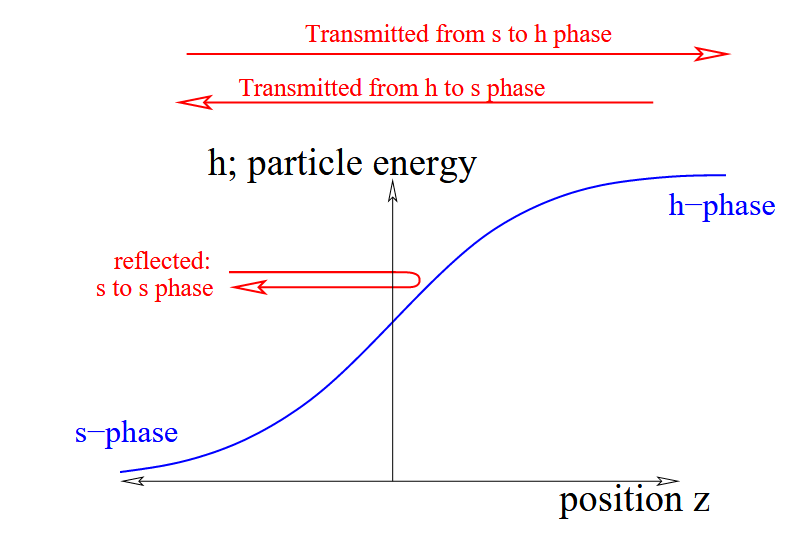
假定泡壁能在极短的时间内被加速到接近光速,于是就算泡泡刚产生时可能不适用于薄壁近似,在被加速一段时间后,泡壁宽度与泡泡半径的比值$\Delta l /R$也会变得很小,此时便可使用薄壁近似。需要注意的是,在泡壁速度还未达到极端相对论时,可能会在一开始的膨胀过程发生一些non-trivial的事情,比如可能在膨胀初期流体阻力能和真空能差值相当,从而在泡壁速度没那么大的情况下便达到平衡。但是在这方面还没有多少比较细致的研究,在此暂且放过不论。在这里我们follow Ellis 和 Lewicki的三篇文章(1809.08242 & 1903.09642 & 2007.15586),但是其中有不少需要商榷的点,有待仔细考虑。
在薄壁近似下,相对论的泡壁的拉氏量可以写为
$$ \mathcal{L}=-4 \pi \sigma R^2 \sqrt{1-\dot{R}^2}+\frac{4 \pi}{3} R^3 p $$
其中$\sigma$是泡壁的表面张力,$p$是泡壁两侧的压力差。上式第一项是动能项,为静止能量除以洛伦兹因子$\gamma = \frac{1}{\sqrt{1-v_w^2}} = \frac{1}{\sqrt{1-\dot{R}^2}} $
根据拉氏量,可以写出关于$\gamma$的运动方程
$$ \frac{\mathrm{d} \gamma}{\mathrm{~d} R}+\frac{2 \gamma}{R}=\frac{p}{\sigma} $$
真空通过鞍点子跃迁到新真空时,由于鞍点子是“不稳定的静态解”,场在时间维度上的导数为0,真空泡泡在产生的瞬间的膨胀速度为0。于是得到上面运动方程的初始条件:在膨胀开始时,$\gamma=1$,泡泡半径$R=R_0$,可以解出
$$ \gamma=\frac{p R}{3 \sigma}+\frac{R_0^2}{R^2}-\frac{p R_0^3}{3 \sigma R^2} \approx \frac{2 R}{3 R_0}+\frac{R_0^2}{3 R^2} $$
后一步用到了鞍点子在薄壁近似下的$R_0=\frac{2 S_1}{\epsilon}=\frac{2 \sigma}{p}$。从上面式子可以看出,当真空泡泡膨胀到一定程度后,有$\gamma \approx \frac{2 R}{3 R_0}$的关系。
现在我们来考虑真空泡两侧的压力。除了真空能量差之外,泡壁会受到来自粒子碰撞的阻力(0903.4099 & 1703.08215)。需要注意的是在此处我们是从粒子的角度出发的讨论,$\Delta V$为零温下的新旧真空势能差,有限温度下的粒子相关的项都并入了阻力项的讨论中。
$$ p = \Delta V- P_{1 \to 1} -P_{1 \to N} $$
$P_{1\to 1 }$可以理解为,随着真空泡膨胀,粒子从假真空进入真真空,由无质量的变为有质量的,这个质量差导致的能量差就来源于泡壁的动能,是一个只和质量差与温度的项。早期仅考虑该领头阶的贡献,将$\Delta V > P_{1 \to 1}$的情景称为是“Runaway”。在本节的讨论中,我们默认$\Delta V > P_{1 \to 1}$
$$ P_{1\to 1} = \frac{1}{24} \Delta m^2 T^2 $$
除了粒子透射外,大质量规范玻色子(如$W/Z$玻色子)在进入泡泡后获得质量,由于其十分不稳定,在泡壁附近发生衰变/跃迁,同样会构成真空泡膨胀的阻力,和泡壁速度有关。有文章认为其和$\gamma$成正比(1703.08215 & 2112.07686),而有的文章认为其和$\gamma^2$成正比(2007.10343)。
$$ P_{1 \to N} = g \gamma^n ~~(n=1或2) $$
由于阻力的次领头项和$\gamma$相关,所以当$\gamma$足够大的时候,必然能使泡泡的阻力和驱动力平衡。$p = \Delta V- P_{1 \to 1} -P_{1 \to N} = 0$的解为泡壁膨胀的终端速度
$$ \gamma_{eq} = \sqrt[n]{\frac{\Delta V - P_{1 \to 1}}{P_{1 \to N}/\gamma^n}} $$
于是可以得到在真空泡膨胀过程的$\gamma$的近似关系
$$ \gamma = \min \left(\frac{2 R}{3 R_0},\gamma_{eq} \right) $$
对于$R_0$,为真空泡泡产生时的大小。由于在相变过程中,真空泡泡在不同温度下随机产生,然后膨胀。我们很难找到准确的在$T_p$温度下所存在的泡泡的初始半径的分布。对于$R_0$的一个比较好的估算方法是使用在成核温度$T_n$下的 bounce 解,找到场值$\phi$为中值的半径位置,作为泡泡产生时的半径。
引力波是由能量波动引起的,在讨论相变过程的引力波,我们需要关注真空跃迁释放的能量都去哪了,哪些会产生怎样的引力波。在这里讨论的过冷相变,核心思想是:在当泡泡仍在加速膨胀时,真空跃迁释放出的真空能,除了抵抗阻力以外,几乎全被用来加速泡壁膨胀,能量几乎全部分布在泡壁。也就是说,当$\gamma<\gamma_{eq}$时,有
$$ \frac{E_{wall}}{E_{V}} = \frac{\Delta V - P_{1\to 1} - P_{1 \to N}}{\Delta V} $$
上面的式子只是表示能量的流向,对于实际的泡壁中的能量,在 2007.15586 中有一十分令人疑惑的关系
$$ E_{wall} = 4 \pi R^2 \int_0^R \frac{\dd r}{3} [\Delta V - P_{1 \to 1} -P_{1 \to N}(r)] $$
这一式子的由来可能是$E_{wall} = 4 \pi R^2 \gamma \sigma$。而结合$\gamma \sim 2R/3R_0$和关于$\gamma$的运动方程
$$ \frac{\mathrm{d} \gamma}{\mathrm{~d} R}+\frac{2 \gamma}{R}=\frac{p}{\sigma} $$
于是可以得到近似关系
$$ \sigma \frac{\dd \gamma}{\dd r} = \frac 1 3 [\Delta V - P_{1 \to 1} -P_{1 \to N}(r)] $$
于是便可以得到上面的泡壁能量关系式。但是同理,我们也可以得到$\frac{\gamma}{r}=\frac{\dd \gamma}{\dd r}$,于是我们完全可以把这式子里的积分给去掉。只能说这个式子比较神秘,需要打一个问号。
现在我们定义一个常数$\alpha_{\infty}$
$$ \alpha_{\infty} = $$
