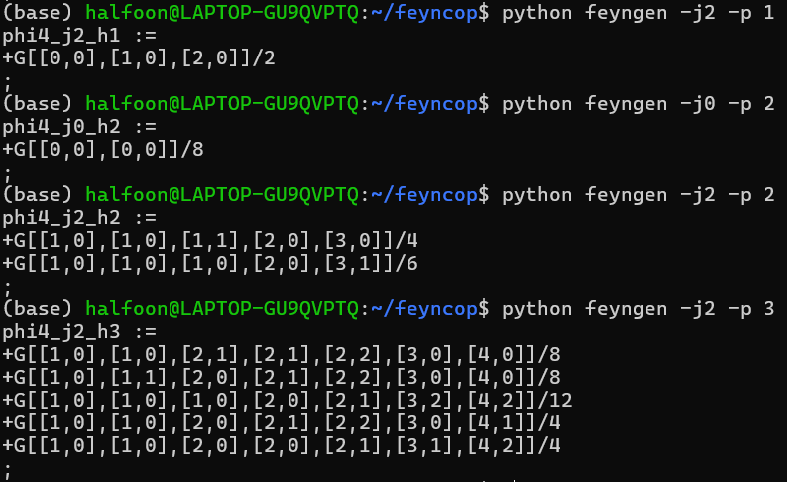
计算费曼图的对称因子实在不是一个轻松的话题,Peskin的书中就直言
“Most people never need to evaluate a diagram with a symmetry factor greater than 2 ,so th ere’s no need to worry too much about these technicalities.”
虽然,事实也是如此,但是真要碰上,那可要头疼一会了(就像我现在这样)。
那么,到底什么是对称因子呢?我们又要如何计算对称因子呢?网络上的讨论充斥着数学家的炫技和初学者的瞎蒙,实在令人头大。希望这篇文章能够稍微讲明白一点点。
什么是对称因子
这个问题可能太简单了。对称因子无非就是消除在计算时对费曼图的重复计数。好,问题来了,是在计算什么的时候呢?让我们从头讲起。
在量子场论中,我们十分关心散射问题,计算散射问题时,无论是通过路径积分还是正则量子化来表述,都要计算格林函数,也即n点关联函数,才能导出散射振幅来计算散射截面等结论。
在路径积分表述下,n点关联函数可以表示为
$$ \begin{aligned} G_n(x_1,...,x_n) & = \eval{\frac{\delta^n}{i^n \delta J(x_1)...\delta J(x_n)} \int \mathcal D \phi~ e^{i \int dx[\mathcal L + J(x)\phi(x)]}}_{J=0}\\ & = \int \mathcal D \phi e^{i \int d^4x \mathcal L}\phi(x_1)\phi(x_2)...\phi(x_n) \\ & =\left \langle \phi(x_1) \phi(x_2) ... \phi(x_n) \right \rangle = \begin{cases} 0 ~~ n为奇数\\ \sum_{wick}(G(a,b)...G(c,d))~~ n为偶数 \end{cases} \end{aligned} $$
也即奇数点的Green函数为0,偶数点的Green函数为各点所有可能的无向连接的2点Green函数乘积之和。这种求和方式被称为Wick求和(虽然除了王正行以外几乎没有书用这种说法就是了)。
而在正则量子化的表述下,n点关联函数可以表示为
$$ \begin{aligned} G(x_1,...,x_n) & = \bra{\Omega} T{\phi(x_1)...\phi(x_n)} \ket{\Omega}\\ & = \frac{\bra{0} T{\phi(x_1)...\phi(x_n) exp[-i\int \dd T H_I]} \ket{0}}{\bra{0} T{\phi(x_1)...\phi(x_n)} \ket{0}} \end{aligned} $$
在微扰展开下,使用正则量子化的表述更为清晰,下面我们则使用正则量子化的语言。(注:不使用路径积分的原因是在考虑相互作用时,需要在生成泛函中引入外源并证明自由场的生成泛函是高斯积分,从而将相互作用项的场算符变为对外源的求导。这一过程中需要对不同的场的拉氏量进行分类讨论,不具备普适性,并且对外源求导的过程中很难看出物理上的对称性。)那么我们要对什么进行展开呢,很显然上述n点关联函数的表达式里出现了指数,我们是在对相互作用项,也即对相互作用系数进行展开。
$$ \bra{0} T{\phi(x_1)...\phi(x_n) exp[-i\int \dd T H_I]} \ket{0} = \bra{0} T{\phi(x_1)...\phi(x_n) [1 - i\int \dd T H_I + ...]} \ket{0} $$
对于第0阶,对于的就是自由场的传播,不存在相互作用。现在来看第一阶,为方便举例,这里就取$\phi^4$的两点关联函数,利用Wick定理可以进行缩并
$$ \begin{aligned} G_1(x,y)*C & = \bra{0} T{\phi(x)\phi(y) (-i) \int \dd t \int \dd[3] z \frac{\lambda}{4!} \phi^4 } \ket{0}\\ & = \frac{-i\lambda}{4!}\bra{0} T{\phi(x)\phi(y) \int \dd t \int \dd[3] z \phi(z)\phi(z)\phi(z)\phi(z) } \ket{0}\\ & = \frac{-i\lambda}{4!} [3*D_F(x-y) \int \dd[4] z~ D_F(z-z)D_F(z-z) + 12* \int \dd[4] z~ D_F(x-z)D_F(y-z)D_F(z-z)] \end{aligned} $$
这里第一个$3$的因子来源是$\phi(x)$和$\phi(y)$组合,剩下4个$\phi(z)$两两组合成为两个无序对,有3种不重复的组合方式。第二个$12$的因子来源是$\phi(x)$和$\phi(z)$有4种组合方式,而$\phi(y)$和剩下3个$\phi(z)$组合有3种组合方式,于是得到12。示意图可以画成这样,组合方式就请读者自己想象一下了。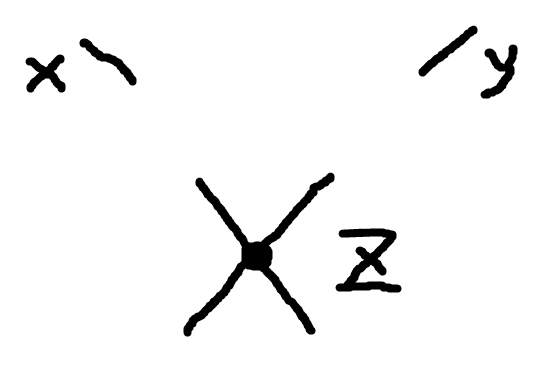
第二阶的展开式,则具有两个$\lambda$
$$ \begin{aligned} G_2(x,y)*C & = \frac{1}{2!} (\frac{-i\lambda}{4!})^2 \bra{0} T{\phi(x)\phi(y) \int \dd[4] u \phi(u)\phi(u)\phi(u)\phi(u) \int \dd[4] w \phi(w)\phi(w)\phi(w)\phi(w)} \ket{0}\\ \end{aligned} $$
对于这个图,其组合方式有点多了,这里就不展开写了。但是我们可以发现,这里的$u$和$w$是等价的,交换这两的记号没有任何物理的可观测效应,同时,Wick缩并两两连接产生的是无序对。于是我们可以得到一个很重要的结论:顶点和内线是不可分辨的。
那么既然顶点是不可分辨的,那么n个顶点交换会产生$n!$个排列方式,正好与泰勒展开的系数$\frac{1}{n!}$相抵。同时,每个顶点的4个$\phi$也是不可分辨的,于是顶点上的4条线来自不同的地方时也会贡献$4!$的因子,正好与相互作用的耦合系数中的$\frac{1}{4!}$相抵(实际上就是为了将系数消去所以才在势场中写下$\frac{1}{4!}$的因子的)。于是,看起来十分完美,常数因子都被我们干掉了,大胆地写出费曼规则中顶点的贡献是一个$-i\lambda$。
但是这样的做法是有问题的,还记得我们前面一阶展开的结果吗?由于有顶点上的4个$\phi$相互连接,所以$4!$会造成重复计数。所以我们需要将重复计数给除掉,这就是对称因子的作用。重复计数不光是一个顶点上的相互连接会产生,两个顶点若有多条内线相连接也会出现。一言蔽之:对称因子是用来修正圈图的贡献系数的。
怎么算对称因子
1.瞪眼法
前面提到了,我们是假设了每个顶点上的4条线连接到的地方都不一样所以每个顶点的4个$\phi$交换会贡献$4!$的系数,那么当一个顶点上的多条线连到了等效的不可区分的地方时,则$4!$会重复计数,需要将多计算的图恢复回去。基于这一想法,我们就可以瞪眼瞪出答案啦!(???)
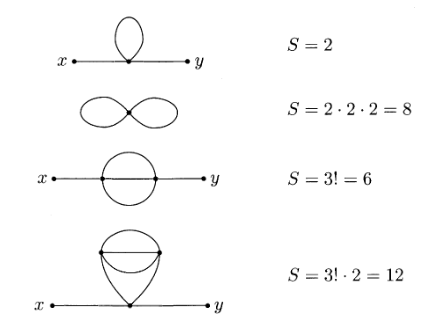
比如这张图,图1在一个顶点上有一个圈,圈的两端与顶点连接的$\phi$交换并不会带来新的图,所以对称因子为$S=2$;图2有两条连接到同一个顶点的内线,这两条内线贡献$2*2$,同时注意到这个图除了这个样子,旋转90度的连接方式同样是一个图,所以还要乘2,对称因子为$S=2*2*2$;图3的两个顶点间有三条不可分辨的内线连接,三条内线交换不变,对称因子为$S=3!=6$;图4和图3类似,但是没与外线连接的两个顶点也是不可分辨的,所以交换还会贡献一个2,所以对称因子为$S=2*3!=12$。
好吧好吧,这样说肯定总是不太令人放心,所以还有个方法!那就是写Wick收缩!一写一算就放心了!
2.数学人的喃喃低语
首先,我不会数学。所以这里我就空着了。但是那些搞群论图论的家伙是能说出个一二三四的。
3.万无一失:上程序
实在算不出,或者不放心,咱就用程序吧,别自个为难自个了。
集美们,这个宝藏软件也太好用了吧!本人无意中发现了可以用来生成费曼图并计算对称因子的软件:feyngen,项目主页参见https://github.com/michibo/feyncop,相关文档则在https://michaelborinsky.com/static/feyngencop_manual.pdf。这玩意本意是用来计算些别的东西的,但是嘛用来算对称因子意外的很好用。使用这个软件,很轻松就能得到我们上面附图举的4个例子的对称因子