有效势

在研究连续对称性自发破缺时，我们需要用一些手段来找到势场的极小值点，来确定背景场（也即“经典场”）的取值。为此我们需要一个称为有效势的函数。有效势的概念由Schwinger等人发展而来，而Jona-Lasinio等人将其运用与研究对称性自发破缺。

此处定义场为$\phi$，经典场为$\phi_c$，经典场的真空期望值为背景场$\phi_\text{bg}$

此处我们使用路径积分的语言，在具有外源$J(x)$的情况下生成泛函为

$$ Z[J] = \bra{0,-\infty}\ket{0,+\infty}_J = e^{iW[J]}= \int \mathcal D \hat \phi~ e^{i[S + J(x)\phi(x)]} $$

可以将联通图的生成泛函$W[J]$做级数展开

$$ iW[J] = \sum_{n=0}^\infty \frac{i^{n}}{n!} \int dx_1 ... dx_n G_c(x_1,...,x_n)J(x_1)...J(x_n) $$

这里的$G_c(x...)$为联通图的格林函数。

场在一定外源$J$下的期望值被定义为经典场$\phi_c(x)$

$$ \begin{aligned} \phi_c(x) & = \langle \phi(x) \rangle_J\\ & = \left[ \frac{\bra{0,-\infty} \phi(x) \ket{0,+\infty}}{\bra{0,-\infty}\ket{0,+\infty}} \right]_J\\ & =\frac{\int \mathcal{D} \phi \phi(x) e^{i\left(S[\phi]+\int d^{4} x J(x) \phi(x)\right)}}{\int \mathcal{D} \phi e^{i\left(S[\phi]+\int d^{4} x J(x) \phi(x)\right)}}\\ & = \fdv{W}{J(x)} \end{aligned} $$

最后一个等式$\phi_c(x) = \fdv{W}{J(x)}$利用$W$的定义不难得到。这一式子说明了生成泛函的对外源的变分对应着场的期望值。亦即当外源为某值时，场处于期望值时，生成泛函取极值，体系处于稳定态（maybe真空态）

而有效作用量（"effective action"）$\Gamma[\phi_c]$定义为生成泛函$W$的勒让德变换

$$ \Gamma[\phi_c] = W[J] - \int \dd[4]{x} J(x) \phi_c(x) $$

于是现在有

$$ \fdv{\Gamma}{\phi_c(x)} = -J(x) $$

若我们把外源$J(x)$取为0，那么有效作用量满足

$$ \eval{\fdv{\Gamma}{\phi_c(x)}}_{\phi_c=\phi_{sol}} = 0 $$

此时对应着的方程的解$\phi_{sol}$则是没有外源下的有效势的极值点，也即体系的稳定状态。对于一般而言具有平移不变性的真空态，$\phi_{sol}$则与空间位置$x$无关，成为一常数，我们可以将其称为背景场$\phi_{bg}$。而有时该方程会有与空间位置有关的解，这些解被称为孤子（soliton）解。

那么现在问题就在于有效作用量的表达式了。实际上，类似于生成泛函$W$的展开，可以将$\Gamma[\phi_c]$展开为

$$ i\Gamma[\phi_c] = \sum_n \frac{1 }{n!} \int \dd[4]x_1 ... \dd[4]x_n i\Gamma^{(n)}(x_1,...,x_n) \phi_c(x_1) ... \phi_c(x_n) $$

其中$i\Gamma^n$为带有n条外线的单粒子不可约（one-particle irreducible / 1PI）格林函数（证明可见 Peskin 7.2及11.4，这里就当结论接受也可），也即所谓的正规顶点，这样便将有效势和费曼图联系在了一起，可以进行微扰论的计算了。

最后，我们定义有效势$V_\text{eff}(\phi_c)$

$$ \Gamma[\phi_c] = - \int \dd[4]x V_\text{eff}(\phi_c) $$

根据上面$\Gamma[\phi_c]$的展开式，可以得到$V_\text{eff}(\phi_c)$的表达式

$$ V_\text{eff}(\phi_c) = - \sum^{\infty}_{0} \frac{1}{n!} \phi^n \Gamma^{(n)} $$

注意，由于$\phi_c$对应着真空态，根据上式进行费曼图的计算得到有效势$V_\text{eff}(\phi_c)$时，需要将外线的动量取为0.

按圈展开

计算有效势我们还是得用微扰论，那么问题来了，我们应该对什么进行展开？这里给出的思路是按圈展开。

对于经典的对称性自发破缺的标量场，势能为四线性的，具有$\phi^4$的形式，在费曼图中，相互作用顶点有4条线。如果我们将普朗克常数放回生成泛函里，那么将不难看出在费曼图中，顶角具有$\hbar^{-1}$的系数，传播子则具有$\hbar$的系数。对于树图，单粒子不可约的图只有一个，如下

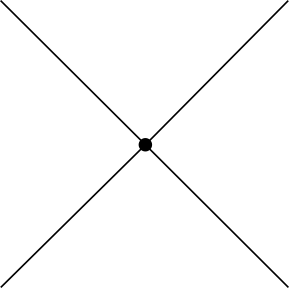
树图具有4条外线，0条内线，1个顶点，所以具有$\hbar^{-1}$的系数。而对于单圈图，如下

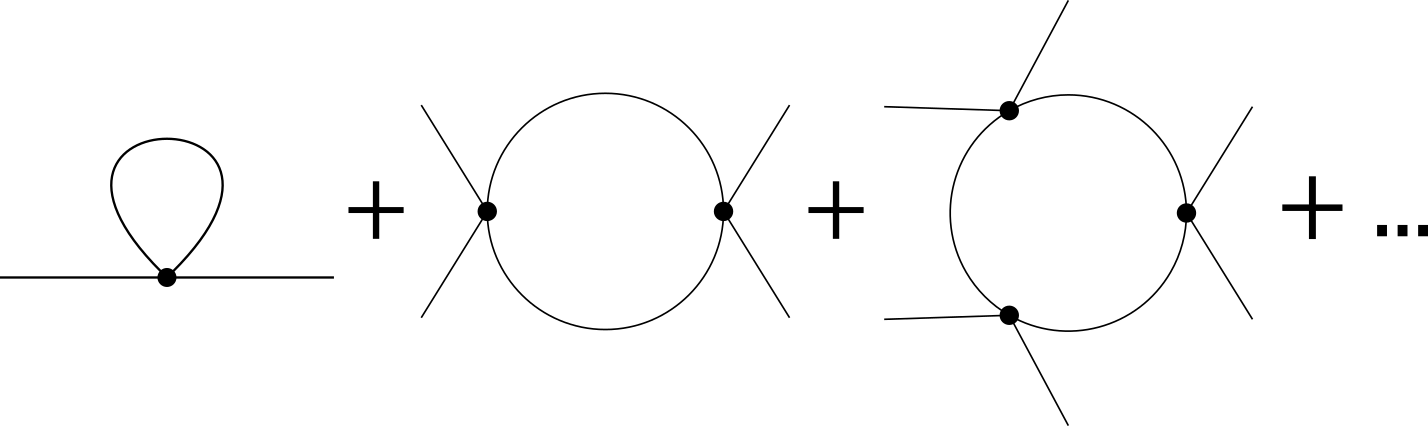
不难发现，传播子和顶点数量相同，具有$\hbar^0$的系数。事实上，从图论不难得知，图的圈数满足$L = I - V + 1$，其中I为内线条数，V为顶点个数。同时不同图的系数中$\hbar$的次数为$H = I - V = L - 1$。于是按圈展开其实本质上是对普朗克常数展开，由于普朗克常数足够小，远小于相互作用的耦合系数，于是这样的展开是一个足够好的展开。这也是为什么在很多研究中树图的精度足以说明问题。

标量场的情况

考虑无质量（或称负质量）的对称性自发破缺的自相互作用的实标量场，拉格朗日密度写为

$$ \mathcal L = \frac{1}{2} (\partial_\mu \phi)^2 + \frac{1}{2} \mu^2 \phi^2 - \frac{1}{4}\lambda \phi^4 $$

注意这里的系数和Coleman文章约定的稍有区别，这样的约定是对复标量场的$\mathcal L = (\partial_\mu \phi^\dagger)(\partial^\mu \phi) - \mu^2 (\phi^\dagger \phi) - \lambda (\phi^\dagger \phi)^2$实化得到的。

那么现在的动量空间的相互作用顶点为$3!*-i\lambda$，传播子为$i/(p^2+i\epsilon)$，另外还需要注意对称因子：外腿固定的情况下上面3个顶点以上的图的对称因子都为1，但是现在的图中的外线的动量都取为$\phi_c$，所以还需要考虑外腿交换的贡献。

1.对于具有n个顶点的图，有2n个外线，这些外线都取为$\phi_c$，之间不可分辨。在可以分辨的情况下，外腿有$(2n)!$种排列方式，但是连接到每个顶点上的两条外线本身是交换不变的，所以每个二元组还要除以2。也即我们应该将2n条外线分为n个无序二元数对，如前所述，这方面贡献因子$\frac{(2n)!}{2^n}$（注意这里是乘，因为外腿是不可分辨的了现在，所以原先外腿取$\phi(1)\phi(2)$和$\phi(2)\phi(2)$这两不一样的图现在都是一样的图，需要乘上将原先的外腿记号交换导致现在的图不变的数量作为因子）。
2.由于这n个顶点在一个环上，所以队头的二元组移到队尾对于现在的费曼图是不变的，这里会贡献一个$\frac{1}{n}$的因子
3.这个环对于镜面翻转还是不变的，所以还会贡献一个$\frac{1}{2}$的因子。
所以要额外乘上的系数为$\frac{(2n)!}{2^n}*\frac{1}{n}*\frac{1}{2}$
示意图如下

于是现在可以写出精确到单圈修正的有效势（当$\mu^2=m^2>0$时）（需要注意的是，根据前面的定义可以看到，联通图的格林函数对应的是$iW$，同样1PI的格林函数对应的其实是$i\Gamma$，需要注意一下这个$i$的因子）

$$ \begin{aligned} V_\text{eff}(\phi_c) & = V_\text{tree} + V_{\text{1loop}}\\ & = \frac{1}{2} \mu^2 \phi_c^2 + \frac{\lambda}{4} \phi_c^4 + i \sum_n \frac{1}{(2n)!} \phi_c^{2n} \frac{(2n)!}{2^n} \frac{1}{n} \frac{1}{2} \int \frac{\dd[4] p}{(2\pi)^4}(-i3!\lambda)^n (\frac{i}{p^2-m^2+i\epsilon})^n \\ & = \frac{1}{2} \mu^2 \phi_c^2 + \frac{\lambda}{4} \phi_c^4 + i \frac{1}{2} \int \frac{\dd[4] p}{(2\pi)^4} \sum_n \frac{1}{n} \left(\frac{3!\lambda \phi_c^2/2}{p^2-m^2+i\epsilon} \right)^n\\ & = \frac{1}{2} \mu^2 \phi_c^2 + \frac{\lambda}{4} \phi_c^4 + \frac{1}{2} \int \frac{\dd[4] p_E}{(2\pi)^4} \sum_n \frac{1}{n} \left(\frac{3\lambda \phi_c^2}{-p_E^2-m^2} \right)^n\\ & = \frac{1}{2} \mu^2 \phi_c^2 + \frac{\lambda}{4} \phi_c^4 + \frac{1}{2} \int \frac{\dd[4] p_E}{(2\pi)^4} \log(1+\frac{3\lambda \phi_c^2}{p_E^2+m^2})\\ & = \frac{1}{2} \mu^2 \phi_c^2 + \frac{\lambda}{4} \phi_c^4 + \frac{1}{2} \int \frac{\dd[4] p_E}{(2\pi)^4} \log(p_E^2+m^2+3\lambda \phi_c^2) + \text{const} \end{aligned} $$

这里倒数第三个等式用了Wick转动，$p_E^0 = -ip^0,p_E^i = p^i$，目的是绕开积分的奇点。这里的const是与$\lambda$和$\phi_c$无关的量，可以不用考虑。我们不难注意到：（并令其为：）

$$ m^2(\phi_c) = m^2+3\lambda \phi_c^2 = \dv[2]{V}{\phi_c} $$

于是

$$ V_{1loop} = \frac{1}{2}\int \frac{\dd[4] p_E}{(2\pi)^4} \log(p_E^2+m^2(\phi_c)) $$

这一积分是发散的（好消息是对数函数发散得足够慢，我们似乎可以简单地选取一个“物理的”上限进行截断，就像在计算兰姆位移时那样），为了计算这一发散的积分，我们需要使用重整化。为了不引入过多的新概念和技巧，我们这里姑且使用截断积分上限的方法进行正规化。

对于此次发散的4维对数积分，设截断上限为$\Lambda$

$$ \begin{aligned} \int \dd[4] p_E \log(p_E^2+m^2(\phi_c)) &= \pi^2 \int \abs{p}^2 \dd{\abs{p}^2} \log{(p^2+m^2(\phi_c))}\\ & = \pi^2 \int_{0}^{\Lambda^2} \rho \log{(\rho + m^2(\phi_c))} \dd p \\ & = \pi^2 \eval{\left [\frac{1}{2} (\rho^2 - m^4)\log(\rho + m^2) + \frac{1}{4} (2m^2\rho-\rho^2) \right ] }^{\Lambda^2}_{0}\\ & = \pi^2 \left [\frac{1}{2} (\Lambda^4 - m^4)\log(\Lambda^2 + m^2) + \frac{1}{4} (2m^2 \Lambda^2-\Lambda^4) + \frac{1}{2} m^4 \log(m^2) \right ] \\ \end{aligned} $$

代回到$V_{1loop}$中

$$ \begin{aligned} V_{1loop}& =\frac{1}{32 \pi^2} \frac{1}{2} \left(\Lambda^4\log(\Lambda^2+m^2) - m^4 \log(\frac{\Lambda^2}{m^2}+1) + m^2\Lambda^2 - \frac{1}{2} \Lambda^4 \right)\\ & \sim \frac{1}{32 \pi^2} \frac{1}{2} \left[2m^2\Lambda^2 - m^4 \left(\log(\frac{\Lambda^2}{m^2})+\frac{1}{2}\right)\right]\\ & = \frac{m^2(\phi_c)}{32\pi^2}\Lambda^2 + \frac{m^4(\phi_c)}{64\pi^2}\left(\log(\frac{m^2(\phi_c)}{\Lambda^2}) - \frac 1 2\right) \end{aligned} $$

倒数第二个等式略去了仅含有积分上限的项（没错，直接丢掉独立的无穷大，这就是所谓的“正规化”！（当然我们有更好的方法解决，比如维度正规化。但是在这里，就暂且直接丢掉吧）），上式中出现的$m^2(\phi_c) = m^2+3\lambda \phi_c^2$。

现在的有效势单圈修正项里包含积分上限/截断能标$\Lambda$，为了消去这一积分上限，或者说是给予这一积分上限可观测的物理效应，我们需要引入一些所谓的“抵消项”（"counter term"）。这样做的理由是，在拉格朗日密度里面出现的参数是所谓的“裸参数”，并不是实际观测到的物理量。例如电子质量是一个在低能收敛的物理参量，但是我们没有理由认为电子质量在极高能仍是0.511MeV，我们知道物质的质量来源于相互作用，基本粒子的质量来源于和Higgs粒子的汤川相互作用，而原子的质量则主要来源于原子核内夸克间复杂的强相互作用，那么在高能时，电子所能参与的相互作用更多，耦合系数也会变化，电子质量自然也会发生变化。（让我们假想一个场景吧，电子我们都知道会参与电磁和弱相互作用，也即会与光子和W玻色子相互作用。如果我们把电子放进一个约束装置中，在某点上光子场的取值为定值，表现为一类似与Higgs场的背景场，那么我们再来看电子的拉氏量，则不光Higgs场会赋予其质量，光子场也会赋予其质量）

既然在拉格朗日密度里出现的不是一个实际的物理量（或者说并不总是实际的物理量），同时在计算有效势的时候我们又遇到了圈图的无穷大问题，那么我们可以这样做：把出现在拉氏量的参数分成两部分，一部分是实际的物理的参数，而剩余部分则当成是我们观测不到的东西。那么如果我们现在要重写拉氏量的话，我们依然可以把之前写的记号当成是物理的参数，而所要做的则是在这一参数的基础上，加上一个“抵消项”。于是，我们怎么确定下这个抵消项讷？我们此前计算了有效势，其单圈修正也是一个不物理的发散值，那么我们现在有了多余的自由度来修正这一问题。我们自然地会考虑，有效势应该能给出物理的结果，比如二阶导能够给出粒子的质量。这样的条件便称为重整化条件。

现在我们写出含有抵消项的拉格朗日密度

$$ \mathcal L = \frac{1}{2} Z (\partial_\mu \phi)^2 - \frac{1}{2} \delta m^2 \phi^2 - \frac{\lambda+ \delta \lambda}{4} \phi^4 $$

于是现在的有效势有

$$ V_\text{eff} = \frac 1 2 \delta m^2 \phi_c^2 + \frac{1}{4} (\lambda+\delta \lambda)\phi_c^4 + \frac{3 \lambda \phi_c^2}{32 \pi^2} \Lambda^2 + \frac{9 \lambda^2 \phi^4}{64\pi^2}(\log(\frac{3\lambda \phi_c^2}{\Lambda^2})-\frac 1 2) $$

重整化条件则为

$$ \begin{aligned} \eval{\dv[2]{V}{\phi_c}}_{\phi_c=0} = m_R^2 = 0\\ \eval{\dv[4]{V}{\phi_c}}_{\phi_c=M} = 3!*\lambda_R \\ \end{aligned} $$

分别代表该标量粒子的实际质量（为0）和实际的自耦合系数$3!\lambda$，对于质量的限定在原点；而对于耦合系数，由于有效势的四阶导在原点处存在奇点，于是我们无法在原点处加以限制，只能在偏离原点的某个具有质量量纲的M上加以限定。这就意味着我们现在定义的$\lambda$不是在壳的。

根据重整化条件可以定出重整化参数$\delta m^2$和$\delta \lambda$，并得出有效势

$$ V_\text{eff} = \frac{1}{4} \lambda \phi_c^4 + \frac{9\lambda^2\phi_c^4}{64\pi^2}\left(\log(\frac{\phi_c^2}{M^2})-\frac{25}{6}\right) $$

在不同能标下的$\lambda$根据有效势的表达式也容易得到

$$ \lambda' = \eval{\dv[4]{V}{\phi_c}}_{\phi_c=M'} /3! = \lambda + \frac{1}{64\pi^2}\log(M'^2/M^2) $$

我们可以看到，在有效势的表达式里面出现了负的项，并且同时出现了log项，这都是单圈修正的量子效应导致的。

如果我们想得到自发破缺的对称性，于是要求$\langle \phi_c\rangle \ne 0$，也即有效势的极小值不在原点。通过对有效势求一阶导$\dv{V_\text{eff}}{\phi_c}=0 $，并且我们选取$M=\phi_c$，也即得到在极小值点的$\lambda$的值

$$ \lambda=2\pi^2/3 $$

远远大于1，超出了微扰计算所能允许的范围。这就说明这样的理论如果想要得到对称性自发破缺其实是不能使用微扰计算的，前面我们的计算都是基于微扰计算，现在相当于走进了死胡同。

标量场+规范场的情况

前面我们提到在标量场中，如果考虑单圈修正的有效势，在微扰计算所能允许的范围内，不能产生自发破缺的对称性。在无质量的标量场中我们只有一个参数$\lambda$，在求解极小值点不等于0时，会有$\lambda<\circ \lambda^2$这样的限制，最终的结果是得出的$\lambda$超出了微扰计算的范围。而在标量QED中，也即标量场和规范场的耦合中，我们拥有两个参数$e$和$\lambda$，我们期望通过引入的新场和新参数能够实现单圈修正下的有效势出现自发对称性破缺。

我们写出两个实标量场与规范场耦合的拉格朗日密度（现在更为流行写成复标量场，但是Coleman的文章中如此，为了避免出现系数约定的差异，这里就仍使用Coleman的记号）

$$ \mathcal L = -\frac{1}{4} F_{\mu\nu}F^{\mu\nu} + \frac{1}{2}(\partial_\mu \phi_1 - eA_\mu \phi_2)^2 - \frac{1}{2}(\partial_\mu \phi_2 + eA_\mu \phi_1)^2 -\frac{\lambda}{4!}(\phi_1^2+\phi_2^2)^2 + \text{counter term} $$

费曼规则为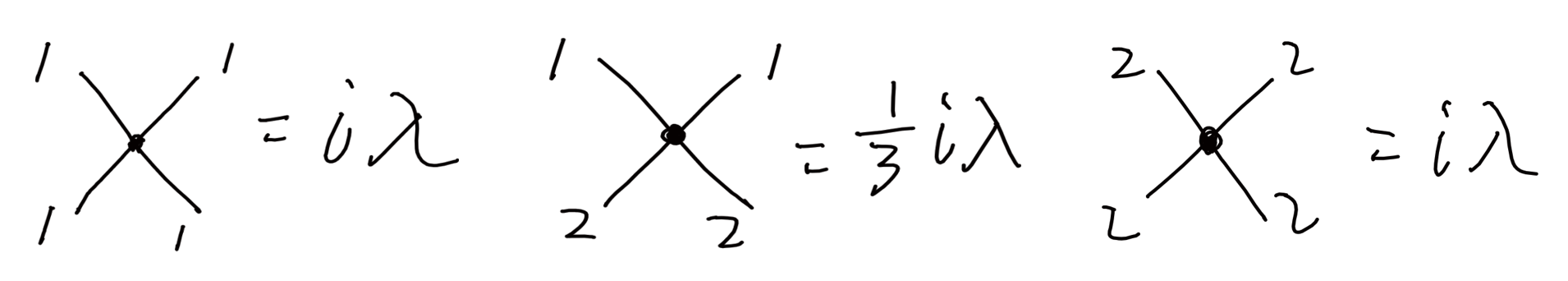

在朗道规范下，光子传播子为

$$ D_{\mu\nu} = -i \frac{g_\mu\nu-k_\mu k_\nu /k^2}{k^2+i\epsilon} $$

三线顶点为

$$ -ie(p^\mu +q^\mu) $$

四线顶点为

$$ 2e^2 g^{\mu\nu} $$

由于在计算有效势时，外线动量取为0，故很容易便可证明包含三线顶点的1PI单圈图贡献都为0。现在单圈修正下的有效势由以下几部分构成，分别是树图贡献，实标量场的自耦合(1)和互耦合(2)，以及标量场与规范场的耦合(3)。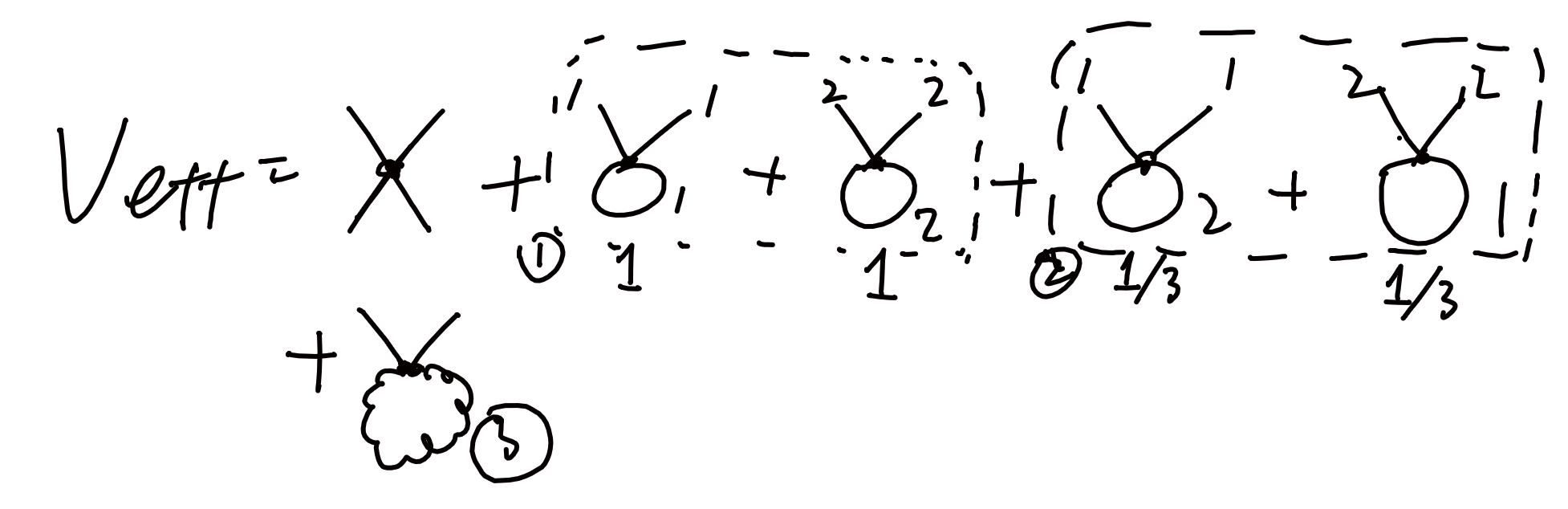

我们不难注意到，$\phi_c^2 = \phi^2_{1c} + \phi^2_{2c}$。(1)和(2)的计算重复下前节的步骤即可，只是替换一下系数。(1)只需要把上一节中的$3!\lambda$换成是$\lambda$，(2)则是把$3!\lambda$换成是$\lambda/3$。现在我们来单独计算(3)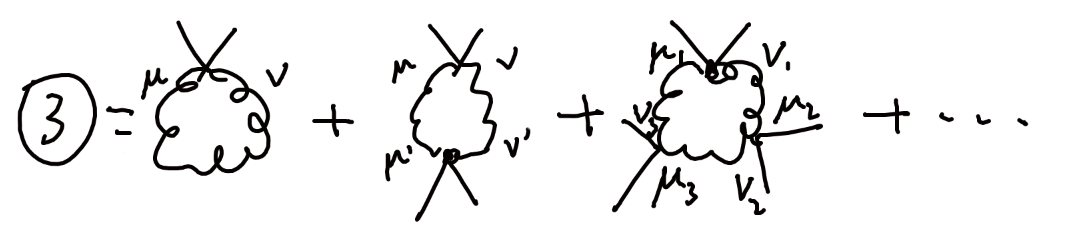

$$ \begin{aligned} (3)& = \cdots * \left[g^{\mu\nu}\frac{g_{\mu\nu} - k_\mu k_\nu/k^2}{k^2+i\epsilon} + g^{\mu\nu}g^{\mu'\nu'}\frac{g_{\mu\nu} - k_\mu k_\nu/k^2}{k^2+i\epsilon}\frac{g_{\mu'\nu'} - k_\mu' k_\nu'/k^2}{k^2+i\epsilon} + g^{\mu\nu}g^{\mu1\nu1}g^{\mu2\nu2} \frac{g_{\mu\nu} - k_\mu k_\nu/k^2}{k^2+i\epsilon} \frac{g_{\mu1\nu1} - k_{\mu1} k_{\nu1}/k^2}{k^2+i\epsilon} \frac{g_{\mu2\nu2} - k_{\mu2} k_{\nu2}/k^2}{k^2+i\epsilon} + \cdots \right]\\ & = \cdots * \left[ g^\mu_\mu - k^\mu k_\mu/k^2 + (g^\mu_\nu - k^\mu k_\nu/k^2)(g^\nu_\mu - k^\nu k_\mu/k^2) +\cdots \right]\\ \end{aligned} $$

由于$(g^\mu_\nu - k^\mu k_\nu/k^2)(g^\nu_\rho - k^\nu k_\rho/k^2) = g^\mu_\rho - k^\mu k_\rho/k^2$以及$ g^\mu_\mu - k^\mu k_\mu/k^2 = D - 1$，于是上面所有的那一坨密密麻麻的涉及度规的乘积最后得到的都是3。由于每一项的系数都是3，于是我们可以直接套用上一节的结果，无非是把$3!\lambda$换成是$2e^2$，并在最外面乘上系数3.于是现在可以写出有效势

$$ \begin{aligned} V_\text{eff} &= \frac{\lambda}{4!} \phi_c^4 + (1) + (2)+ (3)\\ & = \frac{\lambda}{4!} \phi_c^4 + V_\text{1loop}(3!\lambda \to \lambda) + V_\text{1loop}(3!\lambda \to \lambda/3) + 3*V_\text{1loop}(3!\lambda \to 2e^2)\\ & = \frac{\lambda}{4!} \phi_c^4 + \left(\frac{\lambda^2\phi_c^4}{256\pi^2} + \frac{\lambda^2\phi_c^4}{2304\pi^2} + \frac{3e^4 \phi_c^4}{64\pi^2} \right) \left(\log(\frac{\phi_c^2}{M^2})-\frac{25}{6}\right)\\ & = \frac{\lambda}{4!} \phi_c^4 + \left(\frac{5\lambda^2\phi_c^4}{1152\pi^2} + \frac{3e^4 \phi_c^4}{64\pi^2} \right) \left(\log(\frac{\phi_c^2}{M^2})-\frac{25}{6}\right)\\ \end{aligned} $$

在现在的有效势表达式中，出现的单圈修正项，$\lambda$以2次方的形式出现，而$e$以4次方的形式出现。在目前的讨论中，此两个参数在物理上没有关联，没有理由认为$e$和$\lambda$是同量级的。如果我们现在来关注体系真空附近的物理，也即取$\langle \phi_c \rangle=M$，$\phi_c \sim \langle \phi_c \rangle$，并假设此理论是可微扰的，于是$\lambda^2$部分的单圈修正远远小于树图。现在可以把有效势写为

$$ V_\text{eff} = \frac{\lambda}{4!} \phi_c^4 + \frac{3e^4 \phi_c^4}{64\pi^2} \left(\log(\frac{\phi_c^2}{\langle \phi_c \rangle^2})-\frac{25}{6}\right) $$

我们若想得到自发破缺的对称性，那么有效势的极小值不在原点，对有效势求一阶导，可以得到

$$ \lambda = \frac{33}{8\pi^2} e^4 $$

要注意的是，这只是在真空附近的参数限制，随着能标变化，$\lambda$和$e$都会跑动，此限制条件不再成立。将此关系代入有效势的表达式中，可以得到真空附近的有效势

$$ V_\text{eff} = \frac{3e^4 \phi_c^4}{64\pi^2} \left(\log(\frac{\phi_c^2}{\langle \phi_c \rangle^2})-\frac{1}{2}\right) $$

有了这一关系，于是我们现在可以考虑此模型中两个粒子的质量问题了，对于标量玻色子

$$ m(S) = \eval{\dv[2]{V_\text{eff}}{\phi_c}}_{\phi_c = \langle \phi_c \rangle} = \frac{3e^4}{8\pi^2}\langle \phi_c \rangle^2 $$

而对于规范玻色子，由于这是一个SU(2)的模型，对称性自发破缺后产生的3个Goldstone玻色子会赋予规范玻色子质量

$$ m(V) = e^2\langle \phi_c \rangle^2 $$

于是

$$ \frac{m^{2}(S)}{m^{2}(V)}=\frac{3}{2 \pi} \frac{e^{2}}{4 \pi} $$

在这一模型中，标量玻色子和规范玻色子的质量比值和场的真空期望值无关，仅依赖于模型参数。这一简单的关系为实验验证提供了很好的途径。

后话

虽然这一基于圈图修正诱导出连续对称性破缺的想法十分美妙，这意味着我们不需要在模型中手放进很多参数和项来构造出树图的破缺，而是通过高阶修正便能自发产生对称性破缺。但是将这套理论放入标准模型中，人们便发现在由于标准模型中的费米子贡献过大，使得单圈修正的有效势是朝负无穷发散的，这显然不是一个好的现象。而近年来，随着引力波探测和相变宇宙学的兴起，人们不断提出一些新物理模型，来解释电弱相变。其中一种解决办法便是引入额外的标量场，通过Coleman势实现自身的对称性破缺，再通过耦合将破缺的对称性传导给希格斯场，从而实现电弱对称性破缺。

仅由Coleman势诱导对称性破缺的准标准模型

在标准模型中，希格斯场的势能是在树图级别被破缺的。现在我们想尝试的是，如果希格斯场的势能在树图是没被破缺的，考虑单圈修正的Coleman势导致希格斯场对称性被破缺的可能性。

所有具有质量的基本粒子都与希格斯粒子发生相互作用，耦合系数正比于粒子质量。于是在标准模型中，我们只需要考虑W/Z玻色子和t夸克这几种质量最大的粒子。

希格斯场是一个自旋为1的二分量旋量场，数学结构容许其具有4个自由度。从原则上考虑，我们计算时需要包含所有的自由度进行计算。但是为了模型的简化程度（我们总是希望有足够简单的模型来描述尽可能多的问题），一般假设对称性被“最大破缺”到我们所需要的能标下的实际的对称性。

考虑最大破缺，希格斯场可以写为

$$ \phi = \frac{1}{\sqrt 2} \binom{\phi^+}{\phi^0} = \frac{1}{\sqrt 2} \binom{0}{\phi_c} $$

于是标准模型中和希格斯场有关的拉格朗日密度为

$$ \begin{aligned} \mathcal L &= \mathcal L_0 + \mathcal L_{IW} +\mathcal L_{IZ} + \mathcal L_{Iq} \\ & = (\partial_\mu \phi_c) (\partial^\mu \phi_c) - \frac{1}{4} \lambda \phi^4_c + \frac{1}{2} \frac{g^2}{2} \phi_c^2 W^+_\mu W^{-\mu} + \frac{1}{2} \frac{g^2+g'^2}{4} Z^\mu Z_\mu \phi^2_c - \frac{Y_q}{\sqrt 2} \bar q q \phi_c \end{aligned} $$

上式中的W和Z两个规范耦合项的第一个$\frac 1 2$来源于希格斯场的幺正规范的$\frac{1}{\sqrt 2}$的平方，而W$\frac{1}{2}$来源于耦合系数的定义带有的$\sqrt 2$。W伴随的T算符只有$T^-T^+$作用在破缺后的希格斯场上不为0，并且贡献为1。而Z项中的$\frac{1}{4}$来源于$T^3$算符作用在希格斯场上并平方产生的。

自耦合项和和W/Z玻色子的耦合项的单圈修正仿照前面的计算结果可以很容易写出

$$ V_{1loop~self+gauge} = \frac{9\lambda^2 \phi_c^4}{64 \pi^2} \left [\log(\frac{\phi_c^2}{M^2})-\frac{25}{6} \right] + \frac{3(2g^4+(g^2+g'^2)^2)}{1024\pi^2}\phi_c^4 \left[\log(\frac{\phi_c^2}{M^2})-\frac{25}{6} \right] $$

对于希格斯场和费米子的汤川耦合对有效势的单圈修正，这里需要做一下计算。从拉格朗日密度里读出费曼规则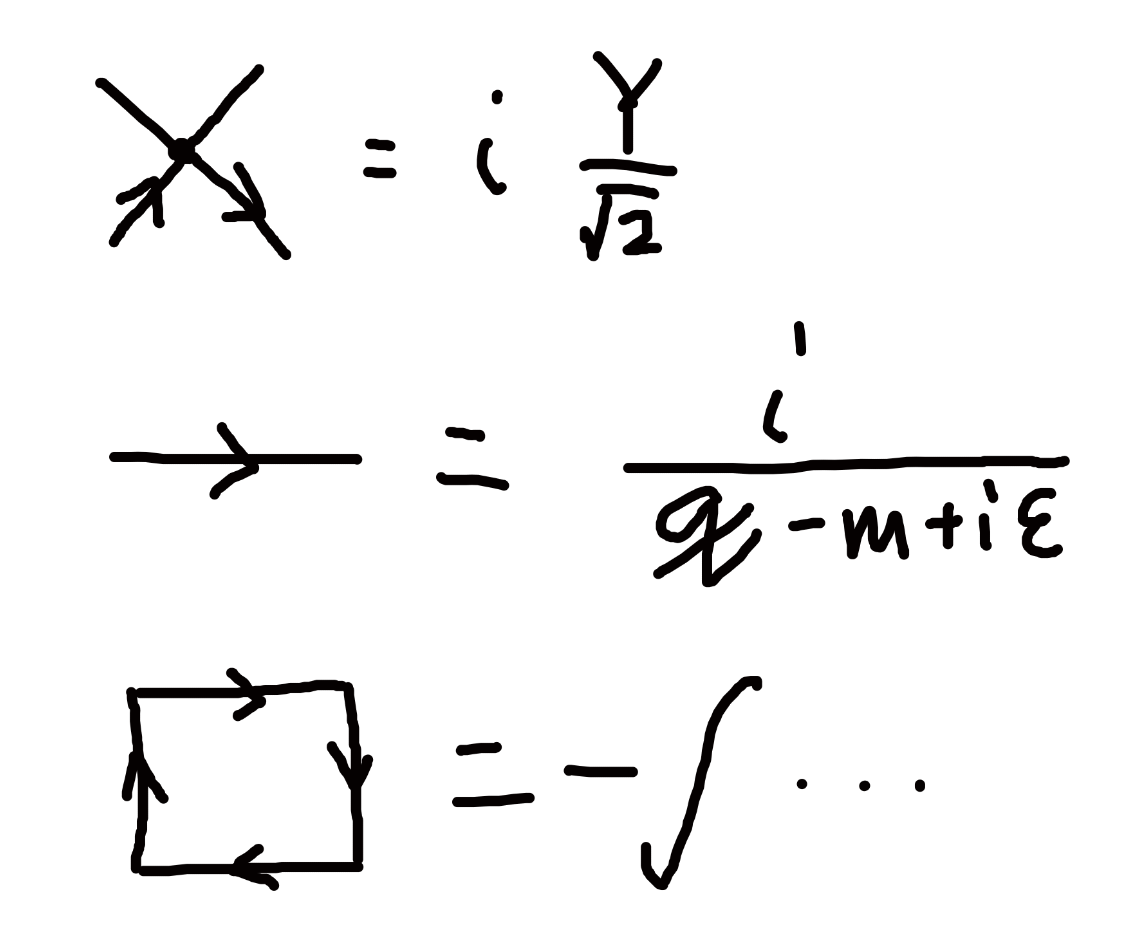

费米子圈会额外多出一个负号，这一性质是费米子交换反对称导致的。用Wick收缩的式子可以明显看出这点。此外，费米子圈另一个需要注意的地方是，奇数个传播子的线的贡献为0，这一点是由于$tr(\gamma^{\mu_1}...\gamma^{\mu_{2n+1}})=0$，并且我们认为夸克/轻子质量是由希格斯机制赋予的，在拉氏量里没有夸克/轻子的质量项。这一结论也被称为Furry定理。此外，在计算对称因子时，需要注意的是，现在单圈图不再具有镜像对称性，或者说图的镜像对称性与费米子的正反粒子的自由度是一个东西，需要避免重复计及。

$$ \begin{aligned} i \Gamma^{(2n)} & = -\frac{(2n)!}{(2n)} \int \frac{\dd[4]q}{(2\pi)^4} (i \frac{q_\mu \gamma^\mu}{q^2+i\epsilon})^{2n} (ig)^{2n}\\ & = -4 \frac{(2n)!}{(2n)} \int \frac{\dd[4]q}{(2\pi)^4} (g^2 \frac{1}{q^2+i\epsilon})^n \end{aligned} $$

$$ \begin{aligned} V_{1loop~feimion} & = - \sum_n \frac{1}{n!} \phi_c^n \Gamma^{(n)}\\ & = -i \sum_n \phi_c^{2n} 4 \frac{1}{2n} \int \frac{\dd[4]q}{(2\pi)^4} (g^2 \frac{1}{q^2+i\epsilon})^n\\ & = -2i \sum \frac{1}{n} \int \frac{\dd[4]q}{(2\pi)^4} ( \frac{g^2 \phi_c^2}{q^2+i\epsilon})^n\\ & = -2i \int \frac{\dd[4]q}{(2\pi)^4} \log(1-\frac{g^2 \phi^2_c}{q^2})\\ & = -2 \int \frac{\dd[4]q_E}{(2\pi)^4} \log(1+\frac{g^2 \phi^2_c}{q_E^2}) \end{aligned} $$

和此前的标量场自耦合以及和规范玻色子耦合的区别在于，费米子耦合的单圈修正对有效势的贡献为负值。后面我们略去重整化的步骤，由于耦合系数$g = Y/\sqrt{2} \propto m_{feimion}$，我们只需要考虑顶夸克的贡献，顶夸克的自由度为$2 \times 2 \times 3$，分别是正反粒子，粒子自旋和色荷的自由度。

$$ V_{1loop~top} = -\frac{3Y_t^2}{64\pi^2} \phi^4_c \left[\log(\frac{\phi_c^2}{M^2})-\frac{25}{6} \right] $$

那么考虑标准模型中的粒子和希格斯场的耦合对有效势的修正的话，单圈修正后的有效势为

$$ \begin{aligned} V_{eff} & = V_0 + V_{self} + V_{gauge} + V_{fermion}\\ & = \frac{\lambda}{4} \phi_c^4 + \frac{9\lambda^2\phi_c^4}{64\pi^2}\left[\log(\frac{\phi_c^2}{M^2})-\frac{25}{6} \right] +\frac{3(2g^4+(g^2+g'^2))}{1024\pi^2}\phi_c^4 \left[\log(\frac{\phi_c^2}{M^2})-\frac{25}{6} \right] -\frac{3Y_t^2}{64\pi^2} \phi^4_c \left[\log(\frac{\phi_c^2}{M^2})-\frac{25}{6} \right] \end{aligned} $$

这里出现的方括号中的常数系数和重整化方案有关。由于对我们现在考虑的问题没有什么影响，这里暂且略去相关的讨论。

由于顶夸克质量比W/Z玻色子质量都要大，并且自由度远远大于这两者，有效势会朝负无穷大发散，导致体系能级没有下限。这显然是不物理的结果，这就说明希格斯的质量并不（或者说可能不完全）是由于单圈修正的Coleman势导致的，我们需要考虑其他的办法来自然地解决希格斯质量的问题。

参考文献

[1] Coleman, Sidney, and Erick Weinberg. “Radiative Corrections as the Origin of Spontaneous Symmetry Breaking.” Physical Review D 7, no. 6 (1973): 1888–1910.
[2] Quiros, Mariano. “Finite Temperature Field Theory and Phase Transitions.” arXiv, January 14, 1999. http://arxiv.org/abs/hep-ph/9901312.
[3] Peskin Chap.11