在今天的宇宙中，我们所能观测到的粒子的质量只占全宇宙物质的5%，而剩下的95%中有70%为暗能量所贡献，还有25%即为所谓暗物质。暗物质的一种可能来源是从热浴中退耦的Freeze Out机制。在极早期宇宙，整个宇宙处于热平衡，暗物质与标准模型的粒子持续地发生相互碰撞和转化而保持平衡。随着宇宙的膨胀，温度逐渐降低，暗物质到标准模型中的粒子的反应被禁闭，暗物质逐渐脱离热平衡，随着宇宙的膨胀被稀释弥散在宇宙各处。

玻尔兹曼方程

让我们先从玻尔兹曼方程开始。玻尔兹曼方程可以写为

$$ \mathbb L[f] = \mathbb C[f] $$

左边为刘维尔项，而右侧为碰撞项。$f(\vb r,\vb p,t)$为分布函数。玻尔兹曼方程描述了粒子的分布函数的演化与粒子在体系中发生的碰撞过程的关系。
在相对论情形下，刘维尔项可以写为

$$ \mathbb L[f] = (p^\alpha \pdv{}{x^\alpha} - \Gamma^{\alpha}_{\beta \gamma} p^{\beta} p^{\gamma} \pdv{}{p^\alpha})f $$

在极早期宇宙，处于热平衡的物质分布均匀且各向同性，于是粒子的分布函数与位置无关，$f(\vb r,\vb p,t)=f(E,t)$。在FRW度规下，刘维尔项可写为

$$ \mathbb L[f] = E \pdv{f}{t} - H \abs{\vb p}^2 \pdv{f}{E} $$

其中$H=\frac{\dot a}{a}$为哈勃常数。考虑到自由度，在坐标空间中的数密度为$n(t) = g/(2\pi)^3 \int \dd[3] p f(E,t)$，于是可以将玻尔兹曼方程改写为

$$ \dv{n}{t} + 3H n = \frac{g}{(2\pi)^3} \int \mathbb C[f] \frac{\dd[3]p}{E} $$

对于粒子$\psi$，考虑碰撞过程$\psi+a+b+\cdots \leftrightarrow i+j+\cdots$，于是上式等式右边为

$$ \frac{g}{(2\pi)^3} \int \mathbb C[f] \frac{\dd[3]p}{E} = \int \dd \Pi_\psi \dd \Pi_a \cdots \dd \Pi_i \cdots (2\pi)^4 \delta^{(4)}(...) \left[\abs{\mathcal M}^2(f_i f_j \cdots - f_\psi f_a f_b \cdots) \right] $$

其中$\dd \Pi_n = \frac{g}{(2\pi)^3} \int \frac{\dd[3] p_n}{2E}$，为相空间体积元，里面包含了粒子的自由度。需要注意的是，这里给出的式子已经做了一定程度的近似，假设了不变振幅的时间反演对称，以及忽略了玻色子和费米子的交换相互作用。
现在我们的玻尔兹曼方程长这样

$$ \dv{n}{t} + 3H n = \int \dd \Pi_\psi \dd \Pi_a \cdots \dd \Pi_i \cdots (2\pi)^4 \delta^{(4)}(...) \left[\abs{\mathcal M}^2(f_i f_j \cdots - f_\psi f_a f_b \cdots) \right] $$

方程左侧描述粒子数密度的演化，方程的右侧则描述了粒子的碰撞导致的粒子数密度变化。方程左侧的第二项描述了宇宙膨胀对粒子数密度的影响，若方程右侧为0，则有$n \propto R^{-3}$。
为了略去宇宙膨胀的影响，可以考虑共动体元的粒子数密度，由于极早期宇宙是一个熵守恒的体系（由于宇宙演化总体上是个准静态过程，但是在发生相变时仍需考虑进熵增），考虑熵密度$s$，则有$sR^3 = \qq*{const}$。于是我们可以定义

$$ Y = \frac{n}{s} $$

对于$Y$，有

$$ \dv{n}{t} + 3H n = \dv{Y}{t} $$

在描述宇宙演化时，以秒计的时间过于抽象且不便，更常用的衡量时间的参量为

$$ x = \frac{m}{T} $$

在辐射主导期间，$T\propto 1/ \sqrt t$（具体关系为$t = 0.301 g_*^{-1/2} m_{pl}/T^2 = 0.301 g_*^{-1/2} (m_{pl}/m^2) x^2$）

所以现在可以将玻尔兹曼方程写为

$$ \dv{Y}{x} = \frac{x}{H(m)s} \int \dd \Pi_\psi \dd \Pi_a \cdots \dd \Pi_i \cdots (2\pi)^4 \delta^{(4)}(...) \left[\abs{\mathcal M}^2(f_i f_j \cdots - f_\psi f_a f_b \cdots) \right] $$

其中$H(m)=1.67 g_*^{1/2} \frac{m^2}{m_{pl}}$为一与哈勃常数相关的数，哈勃常数为$H(x) = H(m) \frac{1}{x^2}$

2->2过程的Freeze Out

现在来考虑最简单的2-2的过程

$$ \psi \bar\psi \leftrightarrow X \bar X $$

这里的$\psi$是我们假定的暗物质粒子，而$X$则是标准模型中的粒子。随着宇宙的膨胀和冷却，$n_\psi$降低，$X$则不再拥有足够的动能，上式反应几乎不再发生，此即Freeze Out。

由于$X$通常除了该反应外，一般同时还参与其他比较强的相互作用，在这个过程中处于热平衡，于是可以分布函数为

$$ f_X=\exp(-E_X/T),~~~f_{\bar X}=\exp(-E_{\bar X}/T) $$

由于能量守恒$E_{X}+E_{\bar X} = E_{\psi}+E_{\bar \psi}$，于是

$$ f_{X}f_{\bar X} = \exp[-(E_X+E_{\bar X})/T] = \exp[-(E_{\psi}+E_{\bar \psi})/T] = f^{EQ}_{\psi}f^{EQ}_{\bar \psi} $$

此处我们定义$f^{EQ}_{\psi} = \exp(-E_\psi/T),~~f^{EQ}_{\bar \psi} = \exp(-E_{\bar \psi}/T)$。

2-2过程的散射振幅为（对初态取自选平均，对末态求和）

$$ \sigma =\frac{1}{g_{\psi} g_{\bar \psi}} \sum_{\psi_{\text{spin}}} \int \frac{(2\pi)^4}{4\sqrt{(p_1 p_2)^2-(m_1 m_2)^2}}\abs{\mathcal M}^2 \dd \Pi_{X} \Pi_{\bar X} $$

于是碰撞项有（为了书写方便，这里动量和质量使用角标1和2来代替$\psi$和$\bar \psi$）

$$ \begin{aligned} \frac{g}{(2\pi)^3} \int \mathbb C[f] \frac{\dd[3]p}{E} &= \int 4 \sigma F (f^{EQ}_{\psi}f^{EQ}_{\bar \psi}-f_{\psi}f_{\bar \psi}) \dd \Pi_\psi \dd \Pi_{\bar \psi}\\ &= \int \sigma v_{\text{Mol}} (\dd n_\psi^{EQ} \dd n_{\bar \psi}^{EQ} - \dd n_\psi \dd n_{\bar \psi}) \end{aligned} $$

其中$F=\sqrt{(p_1 p_2)^2-(m_1 m_2)^2}$，$v_{\text{Mol}} = F / (E_1 E_2)$，$v_{\text{Mol}}$为Moller速度，使用这样定义的速度能够保证整个碰撞项是洛伦兹协变的。

如果我们假设早期宇宙中这样的过程达成热平衡的弛豫时间比化学平衡的弛豫时间要小得多的话，也即发生freeze out后粒子数密度仍然$n \sim \exp(-E/T)$（“From symmetry considerations, the distributions in kinetic equilibrium are proportional to those in chemical equilibrium, with a proportionality factor independent of momentum”），那么可以将碰撞项写为

$$ \frac{g}{(2\pi)^3} \int \mathbb C[f] \frac{\dd[3]p}{E} = \langle \sigma v_{\text{Mol}} \rangle ( n_\psi^{EQ} n_{\bar \psi}^{EQ} - n_\psi n_{\bar \psi}) $$

其中散射截面乘上Moller速度的热平均为

$$ \langle \sigma v_{\text{Mol}} \rangle = \frac{\int \sigma v_{\text{Mol}} \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2}{\int \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2} $$

于是现在玻尔兹曼方程可以写为

$$ \dv{n}{t} + 3Hn = -\langle \sigma v\rangle [n_\psi^2 -(n_\psi^{EQ})^2] $$

$$ \dv{Y}{x} = - \frac{x\langle \sigma v\rangle s}{H(m)} (Y^2 - Y^2_{EQ}) $$

而$Y_{EQ}=n_{EQ}/s$，在$x=m/T\ll 3$的极端相对论和$x=m/T\gg 3$的非相对论情况下为（此处均取玻尔兹曼分布）

$$ Y_{EQ} = 0.145 \frac{g}{g_{*s}}x^{3/2}e^{-x}~~~(x\gg 3) $$

$$ Y_{EQ} = 0.231 \frac{g}{g_{*s}}~~~(x\ll 3) $$

可以注意到，在玻尔兹曼方程中右侧出现的系数$\frac{x\langle \sigma v\rangle s}{H(m)} \propto x^{-2}$，也即随着宇宙的冷却该项迅速降低，$\dd Y/ \dd x \sim 0$，单位共动体积的粒子数密度的演化逐渐停滞，不再变化。
更定量的分析：将玻尔兹曼方程改写为

$$ \frac{x}{Y_{EQ}} \dv{Y}{x} = - \frac{\Gamma}{H} \left[\left( \frac{Y}{Y_{EQ}}\right)^2 -1 \right ] $$

其中$\Gamma = n_{EQ}\langle \sigma v\rangle$，出现在右边的因子$\Gamma/H$为湮灭效率，容易看出当$\Gamma/H <1$时，$Y$的变化也是比较小的量级。

• Hot Relics
  当$\psi$在$x_f \ll 3$时发生freeze out，此时$Y_{EQ}=0.231 {g}/{g_{*s}(x)}$对不显含温度也即$x$，经过一定时间的演化$Y$将演化到$Y_{EQ}(x_f)$，此时发生freeze out。所以

  $$ Y_\infty = Y(x \to \infty) = Y_{EQ}(x_f) = 0.231 {g}/{g_{*s}(x)} $$

  在今天的宇宙，我们所能观测到的物理量粒子数密度$n_{\psi 0}$，质量密度$\rho_{\psi 0}$，在宇宙中的质量占比$\Omega_\psi$为（这里的$h^2$是一个用来消除哈勃常数的测量问题的一个系数，$h=100~\text{km/s/Mpc}$）

  $$ n_{\psi 0} = s_0 Y_\infty = 2970 Y_\infty ~\text{cm}^{-3} $$

$$ \rho_{\psi 0} = n_{\psi 0} m = s_0 Y_\infty m $$

$$ \Omega_\psi h^2 = \frac{\rho_{\psi 0}}{\rho_0}h^2 = \frac{8\pi}{3 M_{pl}^2} \frac{h^2}{H_0^2} \rho_{\psi 0} $$

• Cold Relics
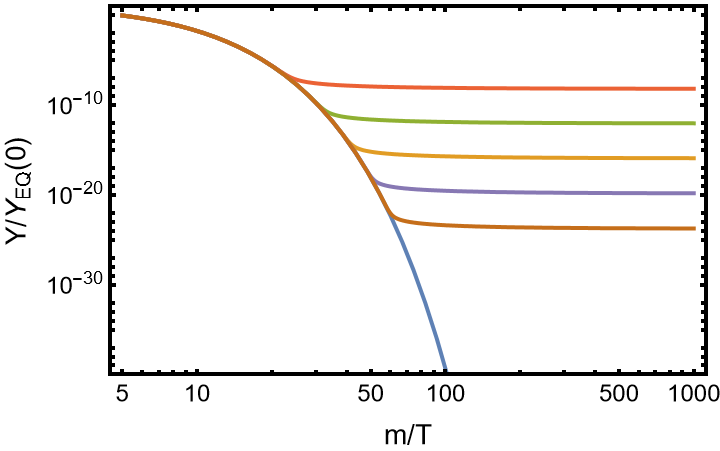
  现在来看freeze out 发生在$x_f > 3$的情况，此时粒子为非相对论的，$Y_{EQ} = 0.145 (g/g_{*s})x^{3/2}e^{-x}$。在这种情况下，$Y_\infty$将严重依赖于freeze out的过程。
  散射截面乘上速度的平均值$\langle \sigma v \rangle$对速度的依赖和反应过程的种类有关，$\langle \sigma v \rangle \propto T^n$，对于s波的湮灭过程$n=0$，对于p波的湮灭过程$n=1$，于是

  $$ \langle \sigma v \rangle = \sigma_0 x^{-n} $$

  于是现在玻尔兹曼方程可以写为

  $$ \dv{Y}{x} = -\lambda x^{-n-2} (Y^2 - Y_{EQ}^2) $$

  其中

  $$ \lambda = \frac{x^3 \sigma_0 s}{H(m)} = 0.264 \frac{g_{*s}}{g_*^{1/2}} M_{pl} m \sigma_0 $$

$\langle \sigma v_{\text{Mol}} \rangle$的计算

如前所述

$$ \langle \sigma v_{\text{Mol}} \rangle = \frac{\int \sigma v_{\text{Mol}} \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2}{\int \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2} $$

为了计算这一积分，需要对体积元进行变换

$$ \dd[3]p_1 \dd[3]p_2 = 4\pi p_1 \dd E_1 4\pi p_2 \dd E_2 \frac 1 2 \dd (\cos \theta ) $$

由于积分$\int \sigma v_{\text{Mol}} \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2$中$\sigma$和$v_{\text{Mol}}$都仅是Mandelstam变量$s$的函数，整个被积函数显含$s$和$E_1+E_2$，于是进一步对体积元进行变换

$$ E_+ = E_1 + E_2 ,~~E_- = E_1 - E_2,~~ s = (p_1+p_2)^2=m_1^2+m_2^2+2E_1 E_2 -2p_1 p_2 \cos \theta $$

使用雅各比矩阵，则有

$$ \begin{aligned} \dd E_+ \dd E_- \dd s &= \abs{\pdv{(E_+,E_-,s)}{(E_1,E_2,\cos \theta)}}\dd E_1 \dd E_2\dd (\cos \theta )\\ & = \begin{vmatrix} 1 & 1 & 0\\ 1 & -1 & 0\\ 2E_1 & 2E_2 & -2p_1 p_2 \end{vmatrix}\dd E_1 \dd E_2\dd (\cos \theta )\\ &=4p_1p_2 \dd E_1 \dd E_2\dd (\cos \theta ) \end{aligned} $$

所以体积元变换为

$$ \dd[3]p_1 \dd[3]p_2 = 2 \pi^2 E_1 E_2 \dd E_+ \dd E_- \dd s $$

要计算的积分现在可以写为

$$ \int \sigma v_{\text{Mol}} \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2 = 2\pi^2 \int \sigma F \exp[-E_+/T] \dd E_+ \dd E_- \dd s $$

注意到$\sigma$和$F$都仅是Mandelstam变量$s$的函数，所以积分顺序应该是$E_-,E_+,s$，可以很容易定出$s$和$E_+$的范围

$$ E+ \ge \sqrt{s} ,~~ s \ge (m_1+m_2)^2 $$

对于$E_-$，由于是最先被积的，需要用$s$和$E_+$来表示，有关系

$$ \begin{aligned} s & = m_1^2 + m_2^2 + 2 E_1 E_2 -2 \sqrt{E_1^2-m_1^2} \sqrt{E_2^2-m_2^2} \cos \theta\\ & = m_1^2 + m_2^2 + \frac 1 2 (E_+^2 - E_-^2) - 2 \sqrt{\left(\frac{E_+ + E_-}{2}\right)^2-m_1^2} \sqrt{\left (\frac{E_+ - E_-}{2} \right)^2-m_2^2} \cos \theta \end{aligned} $$

当$\cos \theta = \pm 1$时，$E_-$取最值。移项并平方后，上面的方程变为$E_-$的二次方程，方程的两根对应最大值和最小值。注意到$F=1/2 \sqrt{s^2-2s(m_1^2+m_2^2)s+(m_1^2-m_2^2)^2}$，则有

$$ \max / \min (E_-) = \frac{(m_1^2 - m_2^2)}{s} \pm \frac{\sqrt{(m_1^2 - m_2^2)^2 - 2(m_1^2 + m_2^2)s +s^2} \sqrt{E_+^2-s}}{s} $$

$$ \frac{(m_1^2 - m_2^2)}{s} - \frac{2F \sqrt{E_+^2-s}}{s} \le E_- \le \frac{(m_1^2 - m_2^2)}{s} + \frac{2F \sqrt{E_+^2-s}}{s} $$

现在我们终于可以积出结果了

$$ \begin{aligned} \int \sigma v_{\text{Mol}} \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2 & = 2\pi^2 \int_{(m_1+m_2)^2}^{\infty} \int_{\sqrt s}^{\infty} \int_{E_{-min}}^{E_{-max}} \sigma F \exp[-E_+/T] \dd E_- \dd E_+ \dd s \\ & = 8\pi^2 \int_{(m_1+m_2)^2}^{\infty} \sigma \frac{F^2}{s} \left(\int_{\sqrt s}^{\infty} \sqrt{E_+^2-s} \exp[-E_+/T] \dd E_+ \right ) \dd s \\ & = 2\pi^2 T \int_{(m_1+m_2)^2}^{\infty} \sigma \frac{s^2-2s(m_1^2+m_2^2)+(m_1^2-m_2^2)^2}{\sqrt{s} }K_1(\sqrt s /T) \end{aligned} $$

这里的$K_1$为第二类修正贝塞尔函数

$$ K_{v}(z)=\frac{\sqrt{\pi} z^{v}}{2^{v} \Gamma\left(v+\frac{1}{2}\right)} \int_{1}^{\infty} e^{-z t}\left(t^{2}-1\right)^{v-\frac{1}{2}} \dd t; \left( \Re(v)>-\frac{1}{2} \bigwedge \Re(z)>0 \right ) $$

而对于分母的计算，则比较容易得到

$$ \begin{aligned} \int \exp[-(E_1+E_2)/T] \dd[3] p_1 \dd[3] p_2 & = \int \exp(-E_1/T) p_1 E_1 \dd E_1 \dd \Omega_1 * \int \exp(-E_2/T) p_2 E_2 \dd E_2 \dd \Omega_2\\ & = [4\pi m_1^2 T K_2(m_1/T)][4\pi m_2^2 T K_2(m_2/T)] \end{aligned} $$

于是我们有

$$ \langle \sigma v_{\text{Mol}} \rangle = \frac{ \int_{(m_1+m_2)^2}^{\infty} \sigma [s^2-2s(m_1^2+m_2^2)+(m_1^2-m_2^2)^2] K_1(\sqrt s /T)}{8 T \sqrt{s} m_1^2 m_2^2 K_2(m_1/T) K_2(m_2/T)} $$

特别的，当$m_1=m_2=m$时

$$ \left\langle\sigma v_{\text{Mol}}\right\rangle=\frac{1}{8 m^{4} T K_2^2(m/T)} \int_{4 m^2}^\infty \sigma \left( s-4 m^2 \right) \sqrt{s} K_{1}(\sqrt{s} / T) \dd s . $$

参考文献

[1] E.W. Kolb, The Early Universe, Front.Phys. 69 (1990) 1-547.
[2] P. Gondolo and G. Gelmini, Cosmic abundances of stable particles: Improved analysis, Nuclear Physics B 360, 145 (1991).