在标准模型中，电弱相关的自由参数有3个，在模型中的自然的选择是$g,~g',~v$。但是这些参数无法被直接测量出，于是我们需要使用精确的实验测量值来定出模型中的参数值。在电弱能标下（即能量标度 $\mu \approx M_Z$），这三个基本输入参数通常选为：

• 电磁精细结构常数（在 $M_Z$ 标度下）：

  $$ \alpha(M_Z) \approx 1/128 $$

• 费米常数（由 $\mu$ 子衰变精确测量）：

  $$ G_F \approx 1.1663787 \times 10^{-5} \, \text{GeV}^{-2} $$

• Z玻色子质量（由 LEP 精确测量）：

  $$ M_Z \approx 91.1876 \, \text{GeV} $$

于是现在我们可以写出其他的参数表达式（follow MadGraph5定义）。在电弱能标（$\mu = M_Z$）的树图阶下

• W 玻色子质量

  $$ M_W= \sqrt{\frac{M_Z^2}{2} \left[ 1 + \sqrt{1 - \frac{4 \pi \alpha(M_Z)}{\sqrt{2} G_F M_Z^2}} \right]} $$

• 电弱混合角

  $$ \sin^2{\theta_w} = 1- \left( \frac{M_W}{M_Z} \right)^2 $$

• 电磁耦合系数

  $$ e = \sqrt{4 \pi \alpha} $$

• 电弱耦合系数$g$（在某些文献中记为$g_W$）

  $$ g = \frac{e}{\sin \theta_W} $$

• 电弱耦合系数$g'$

  $$ g' = \frac{e}{\cos \theta_W} $$

• 希格斯场真空期望值$v_{EW}$

  $$ v_{EW} = 2 M_W \sin{\theta_W}/e = \frac{1}{\sqrt{\sqrt 2 G_F}} $$

以上表达式都只是树图级别的，在单圈/多圈/辐射修正下，需要进行一定的修正，详细可以参考 1902.05142

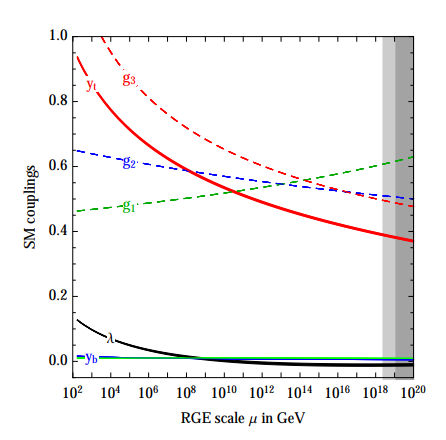
在新物理能标下，理论上我们需要计算参数的跑动。但是$\alpha$的跑动在电弱能标以上很小，在很大的范围中都无需考虑。以下图片来源于 1205.6497，可见在$\mu<10^{10} ~\text{GeV}$的范围，电弱耦合系数的跑动都不超过$ 10\% $，对于目前的新物理讨论可以暂时忽略不计。